Радиус окружности, вписанной в правильный треугольник

Определение и формулы окружности, вписанной в правильный треугольник

ОПРЕДЕЛЕНИЕ

Окружность, касающаяся всех трех сторон треугольника, называется его вписанной окружностью.

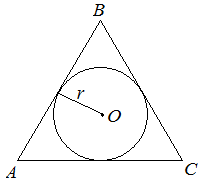
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.

Радиус окружности, вписанной в правильный треугольник, равен

$r=\frac{a\sqrt{3}}{6}$

Примеры решения задач

ПРИМЕР 1

Задание

Найдите площадь треугольника $ABC$ , если радиус вписанной в него окружности равен $3$ см

Решение

Из формулы для радиуса окружности, вписанной в правильный треугольник, найдем длину сторону треугольника

$r=\frac{a\sqrt{3}}{6} \Rightarrow a=\frac{6r}{\sqrt{3}} =\frac{18}{\sqrt{3}} =\frac{18\sqrt{3}}{3} =6\sqrt{3} cm$

Тогда площадь равностороннего треугольника

$S=\frac{a^{2} \sqrt{3}}{4} =\frac{\left(6\sqrt{3} \right)^{2} \cdot \sqrt{3}}{4} =\frac{108\sqrt{3}}{4} =27\sqrt{3} cm ^{2}$

Ответ

$S=27\sqrt{3}$ см $^{2}$

ПРИМЕР 2

Задание

Высота правильного треугольника равна 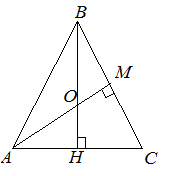$6$ см. Найти радиус окружности, вписанной в этот треугольник.

Радиус окружности, вписанной в правильный треугольник

Решение

В правильном треугольнике $ABC$ опустим высоту $BH=6$ см. Для того, чтобы найти радиус окружности, вписанной в этот треугольник, нужно найти длину его стороны.

Рассмотрим прямоугольный треугольник $ABH$ . Пусть $AB=a$ , тогда $AH=\frac{a}{2}$ (т.к. $ABC$ – правильный и $BH$ – медиана). Тогда теорема Пифагора для треугольника $ABH$ запишется в виде: