Радиус окружности, вписанной в прямоугольный треугольник
Определение и формулы окружности, вписанной в прямоугольный треугольник
ОПРЕДЕЛЕНИЕ
Окружность, касающаяся всех трех сторон треугольника, называется его вписанной окружностью.
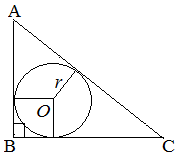
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
Радиус окружности, вписанной в прямоугольный треугольник, равен отношению площади треугольника к его полупериметру:
![\[r=\frac{S}{p} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9d76b85fb36e157625802e1d33df229f_l3.png "Rendered by QuickLaTeX.com")
Есть еще одна формула для вычисления радиуса:
![\[r=\frac{a+b-c}{2} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c7079d4297444877cc397f4b53622c20_l3.png "Rendered by QuickLaTeX.com")
Примеры решения задач
ПРИМЕР 1
| Задание | Площадь прямоугольного треугольника  равна  . Найдите периметр треугольника , если радиус вписанной окружности равен 
|
| Решение | Так как радиус вписанной окружности равен отношению площади треугольника к его полупериметру, то тогда периметр треугольника
|
| Ответ |  см
|
![\[P=2p=\frac{2S}{r} =\frac{64}{4} =16 cm \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fb02383250c55e4565fa29b8d69b48fc_l3.png "Rendered by QuickLaTeX.com")
ПРИМЕР 2
| Задание | В прямоугольном треугольнике с прямым углом  катеты равны 8 см и 6 см. Найти радиус окружности, вписанной в этот треугольник.
|
| Решение | Радиус вписанной окружности равен отношению площади треугольника к его полупериметру:
Найдем площадь заданного треугольника По теореме Пифагора гипотенуза Полупериметр Тогда радиус |
| Ответ |  см
|
![\[S_{ABC} =\frac{1}{2} \cdot AB\cdot BC=\frac{1}{2} \cdot 8\cdot 6=24 cm ^{2} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-177a05bb6bfeb4c59a6c676d760f8fd9_l3.png "Rendered by QuickLaTeX.com")
![\[AC=\sqrt{AB^{2} +BC^{2}} =\sqrt{6^{2} +8^{2}} =10 cm \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1db6987712153cea6ef8bbe31b7d66f3_l3.png "Rendered by QuickLaTeX.com")
равен:![\[p=\frac{AB+BC+AC}{2} =\frac{6+8+10}{2} =12 cm \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4ebfc6627585c3795f01d4cb1f0d29ec_l3.png "Rendered by QuickLaTeX.com")
![\[r=\frac{S}{p} =\frac{24}{12} =2 cm \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-be3fe0dae9934498d58235426af6cb14_l3.png "Rendered by QuickLaTeX.com")
