Радиус окружности, вписанной в равнобедренный треугольник

Определение и формулы окружности, вписанной в равнобедренный треугольник

ОПРЕДЕЛЕНИЕ

Окружность, касающаяся всех трех сторон треугольника, называется его вписанной окружностью.

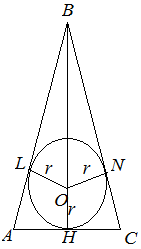
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.

Радиус окружности, вписанной в равнобедренный треугольник, равен отношению площади треугольника к его полупериметру

$r=\frac{S}{p}$

Если обозначить боковые стороны равнобедренного треугольника через $a$ , а основание через $b$ , то

$r=\frac{S}{p} =\sqrt{\frac{(p-a)(p-a)(p-b)}{p}} =\sqrt{\frac{(p-a)(p-a)(p-b)}{p}} =\frac{b}{2} \sqrt{\frac{2a-b}{2a+b}}$

Примеры решения задач

ПРИМЕР 1

Задание

В равнобедренном треугольнике боковые стороны равны 25 см, а основание 30 см. Найти радиус вписанной окружности.

Пример 1, радиус окружности, вписанной в равнобедренный треугольник

Решение

Рассмотрим равнобедренный треугольник $ABC$ с боковыми сторонами $AB=BC=25$ см и основанием $AC=30$ см. Найдем площадь треугольника по формуле Герона:

$S=\sqrt{p(p-AB)(p-BC)(p-AC)} ,$

где полупериметр $p=\frac{AB+BC+AC}{2} =\frac{80}{2} =40$ см. Тогда

$S=\sqrt{40\cdot (40-25)\cdot (40-25)\cdot (40-30)} =300 cm ^{2}$

Тогда искомый радиус

$r=\frac{S}{p} =\frac{300}{40} =7,5 cm$

Ответ

$r=7,5$ см

ПРИМЕР 2

Задание

В равнобедренном треугольнике окружность, вписанная в него, делит в точке касания боковую сторону на отрезки 7 см и 10 см, считая от основания. Найти радиус этой окружности.

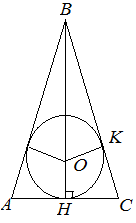
Пример 2, радиус окружности, вписанной в равнобедренный треугольник

Решение

Рассмотрим равнобедренный треугольник $ABC$ с основанием $AC$ , в который вписана окружность. Точка $K$ – точка касания окружности и боковой стороны $BC$ такая, что $BK=10$ см, $KC=7$ см. По свойству отрезков касательных, проведенных из одной точки к окружности,

$CH=CK=7 cm$