Окружность, вписанная в правильный треугольник

Определение и формулы окружности, вписанной в правильный треугольник

ОПРЕДЕЛЕНИЕ

Окружность, касающаяся всех трех сторон треугольника, называется его вписанной окружностью.

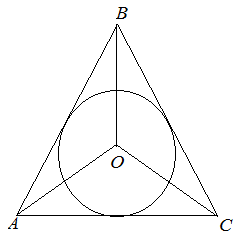
Окружность, касающаяся всех трех сторон треугольника, называется его вписанной окружностью.

Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.

В любой треугольник можно вписать окружность, причем, только одну.

Если окружность вписана в правильный треугольник (в тот, у которого все стороны равны между собой), то ее радиус $r$ вычисляется по формуле

$r=\frac{S}{p} ,$

где $S$ – площадь треугольника, а $p$ – его полупериметр; или его можно выразить через сторону $a$ следующим образом:

$r=\frac{a\sqrt{3}}{6}$

ПРИМЕР 1

Задание	В правильном треугольнике $ABC$ сторона $AB=9$ см. Найти радиус окружности, вписанной в треугольник $ABC$ .
Решение	Поскольку треугольник $ABC$ – правильный, то радиус окружности, вписанной в этот треугольник, найдем по формуле $r=\frac{AB\sqrt{3}}{6} =\frac{9\sqrt{3}}{6} =\frac{3\sqrt{3}}{2} cm$
Ответ	$r=\frac{3\sqrt{3}}{2}$ см