Внешний угол треугольника
Определение и формула внешнего угла треугольника
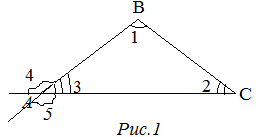
На рисунке 1 внешний угол треугольника ![]() при вершине
при вершине ![]() отмечен номером 4.
отмечен номером 4.
Для внешнего угла треугольника справедливо утверждение: Внешний угол треугольника равен сумме внутренних углов, не смежных с ним:
![]()
Свойства внешнего угла
- Сумма внешнего и внутреннего углов при одной вершине равна
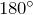 :
: - Сумма внешних углов треугольник взятых по одному при каждой вершине равна
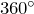 .
. - Внешние углы при одной вершине треугольника равны между собой (как вертикальные):
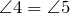 .
.
![]()
Примеры решения задач
| Задание | В треугольнике 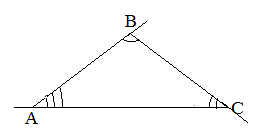
|
| Решение | Сумма углов треугольника Внешний угол при вершине |
| Ответ |
|
| Задание | В треугольнике 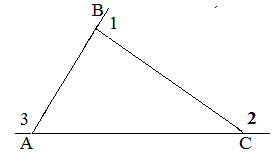
|
| Решение | Обозначим внешний угол при вершине Сумма углов треугольника |
| Ответ |
|











