Высота равнобедренного треугольника
Определение и формулы высоты равнобедренного треугольника
Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
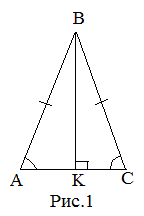
Равные стороны ![]() называются боковыми сторонами, а третья сторона
называются боковыми сторонами, а третья сторона ![]() – основанием треугольника (рис. 1).
– основанием треугольника (рис. 1).
Свойство высоты равнобедренного треугольника: в равнобедренном треугольнике высота, проведенная к основанию, является одновременно и биссектрисой, и медианой треугольника:
![]()
Примеры решения задач
| Задание | В равнобедренном треугольнике |
| Решение | В треугольнике откуда
|
| Ответ |
|
| Задание | В равнобедренном треугольнике |
| Решение | В равнобедренном треугольнике 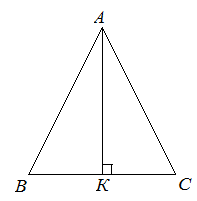
Так как |
| Ответ |
|











