Область значений функции

ОПРЕДЕЛЕНИЕ

Областью значений или областью изменения функции $y=f\left(x\right)$ называется множество значений, которые может принимать зависимая переменная $y$ .

Обозначается область значения функции — $E\left(f\right)$ или $E\left(y\right)$ .

Область значений основных элементарных функций

Для линейной функции 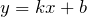$y=kx+b$ область значений $E\left(y\right):y\in R$ .
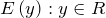Для обратной пропорциональности, то есть функции заданной формулой 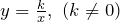$y=\frac{k}{x} ,\ \left(k\ne 0\right)$ , область значений: $E\left(y\right):y\in \left(-\infty ,\; 0\right)\bigcup \left(0,\; +\infty \right)$ .
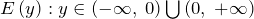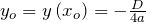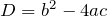Значение $y_{o} =y\left(x_{o} \right)=-\frac{D}{4a}$ , где $D=b^{2} -4ac$ дискриминант, называется ординатой вершины параболы, задаваемой уравнением $y=ax^{2} +bx+c \left(a\ne 0\right)$ .

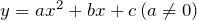Действительно, абсцисса вершины параболы вычисляется по формуле $x_{0} =-\frac{b}{2a}$ , тогда

$y\left(x_{o} \right)=a\cdot \left(-\frac{b}{2a} \right)^{2} +b\cdot \left(-\frac{b}{2a} \right)+c=\frac{ab^{2} }{4a^{2} } -\frac{b^{2} }{2a} +c=\frac{b^{2} -2b^{2} +4ac}{4a} =-\frac{D}{4a}$

Итак, для квадратичной функции $y=ax^{2} +bx+c$ : если $a<0$ , то ветки параболы направлены вниз и значение $y_{o}$ является наибольшим значением функции, то есть $E\left(y\right):y\in \left(-\infty ,\; y_{o} \right]$ ; если $a>0$ , то ветки направлены вверх и значение $y_{o}$ является наименьшим значением функции, то есть $E\left(y\right):y\in \left[y_{o} ,\; +\infty \right)$ .

Для логарифмической функции 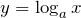$y=\log _{a} x$ область значений $E\left(y\right):y\in R$ .
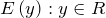Для показательной функции 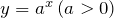$y=a^{x} \left(a>0\right)$ область значений $E\left(y\right):y\in \left(0,\; +\infty \right)$ .
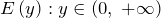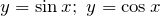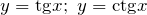Для тригонометрических функции $y=\sin x;\ y=\cos x$ область значений $E\left(y\right):y\in \left[-1,\; 1\, \right]$ , для $y=\text{tg} x;\ y=\text{ctg} x$ область значений — множество всех действительных чисел.

ЗАМЕЧАНИЕ

Нередко при исследовании тригонометрических функций помогает формула

$a\cdot \cos x+b\cdot \sin x=\sqrt{a^{2} +b^{2} } \cdot \cos \left(x-\alpha \right),$

из которой следует, что областью значений функции $y=a\cos x+b\sin x$ является промежуток $E\left(y\right):y\in \left[-\sqrt{a^{2} +b^{2} } ,\; \sqrt{a^{2} +b^{2} } \, \right]$ .

Примеры решения задач

ПРИМЕР 1

Задание

Найти область значений квадратичных функций

$\ 1)\ y_{1} =-x^{2} +4x-3;\ 2)\ y_{2} =x^{2} +2x-5$

Решение

1) Для функции $y_{1} =-x^{2} +4x-3$ имеем, что $a=-1,\ b=4,\ c=-3$ . Графиком этой функции является парабола. Найдем абсциссу вершины параболы

$x_{2} =-\frac{b}{2a} =-\frac{4}{2\cdot \left(-1\right)} =2$

Для нахождения $y_{o}$ подставим найденное значение $x_{o}$ в заданное квадратичное уравнение

$y_{o} =y_{1} \left(x_{o} \right)=y\left(2\right)=-2^{2} +4\cdot 2-3=-4+8-3=1$

Так как $a=-1<0$ , то ветви параболы направлены вниз и область значения $E\left(y_{1} \right):y\in \left(-\infty ,\; 1\right]$ .

2) Для функции $y_{2} =x^{2} +2x-5:\ a=1,\ b=2,\ c=-5$ . Значение $a=1>0$ , значит, ветки параболы направлены вверх, и значение $y_{o}$ является наименьшим значением функции. Найдем это значение:

$y_{o} =-\frac{b^{2} -4ac}{4a} =-\frac{2^{2} -4\cdot 1\cdot \left(-5\right)}{4\cdot 1} =-\frac{4+20}{4} =-6$

Таким образом, $E\left(y_{2} \right):y\in \left[-6,\; +\infty \right)$ .

Ответ

$E\left(y_{1} \right):y\in \left(-\infty ,\; 1\right]; E\left(y_{2} \right):y\in \left[-6,\; +\infty \right)$

ПРИМЕР 2

Задание

Найти область значений тригонометрических функций

$\ 1)\ y_{1} =3\cos x-2;\ 2)\ y_{2} =\cos x\cdot \sin x;\ 3)\ y_{3} =3\cos x-4\sin x$

Решение

1) Для определения области значений функции $y_{1} =3\cos x-2$ используем тот факт, что $E\left(\cos x\right):y\in \left[-1,\; 1\, \right]$ , то есть имеет место двойное неравенство

$-1\le \cos x\le 1$

Умножим все части этого неравенства на 3:

$-3\le 3\cos x\le 3;$

вычтем из всех частей полученного неравенства 2, получим

$-3-2\le 3\cos x-2\le 3-2\Rightarrow -5\le 3\cos x-2\le 1$

Таким образом, $E\left(y_{1} \right):y\in \left[-5,\; 1\right]$ .

2) Для нахождения области значения функции $y_{2} =\cos x\cdot \sin x$ , преобразуем правую часть выражения по формуле синуса двойного угла:

$2\cos x\cdot \sin x=\sin 2x\Rightarrow \cos x\cdot \sin x=\frac{\sin 2x}{2}$

Получим

$y_{2} =\frac{1}{2} \sin 2x$

Учитывая, что $E\left(\sin 2x\right):y\in \left[-1,\; 1\, \right]$ , получаем, что $E\left(y_{2} \right)=E\left(\frac{1}{2} \sin 2x\right):y\in \left[-\frac{1}{2} ,\; \frac{1}{2} \, \right]$ .

3) Для нахождения области значения функции $y_{3} =3\cos x-4\sin x$ , воспользуемся формулой

$a\cdot \cos x+b\cdot \sin x=\sqrt{a^{2} +b^{2} } \cdot \cos \left(x-\alpha \right)$

В нашем случае $a=3;\ b=-4$ , то есть

$3\cos x-4\sin x=\sqrt{3^{2} +\left(-4\right)^{2} } \cdot \cos \left(x-\alpha \right)=\sqrt{9+16} \cdot \cos \left(x-\alpha \right)=5\cos \left(x-\alpha \right)$

Следовательно, областью значений является промежуток $E\left(y_{3} \right):y\in \left[-5,\; 5\, \right]$ .

Ответ

$E\left(y_{1} \right):y\in \left[-5,\; 1\; \right]; E\left(y_{2} \right):y\in \left[-\frac{1}{2} ,\; \frac{1}{2} \, \right]; E\left(y_{3} \right):y\in \left[-5,\; 5\, \right]$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Область значений функции

Область значений основных элементарных функций

Примеры решения задач