Решение неравенств

Определение и формулы неравенств

ОПРЕДЕЛЕНИЕ

Неравенством называется алгебраическое выражение, в котором функции связаны между собой знаками сравнения <, >, $\le ,\; \ge$ .

Знаки <, > называются знаками строгого неравенства, а знаки $\le ,\; \ge$ — знаками нестрогого неравенства.

Если в неравенство входят только числовые величины, то такое неравенство называется числовым неравенством.

ОПРЕДЕЛЕНИЕ

Решением неравенства называется значения переменной, при котором неравенство становится верным.

Решить неравенство — это значит найти множество всех его решений

Неравенства называют равносильными, если они имеют одно и тоже множество решений.

Основные правила, применяемые при решении неравенств

Если какое-либо слагаемое перенести из одной части неравенства в другую, изменив при этом его знак на противоположный, то получим неравенство, равносильное данному.
Если обе части неравенства умножить (разделить) на одно и то же положительное число, то получим неравенство, равносильное данному.
Если обе части неравенства умножить (разделить) на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получим неравенство, равносильное данному.

В зависимости от того, какие функции входят в неравенство, различают линейные, квадратные, дробно-рациональные, иррациональные, логарифмические, показательные неравенства, неравенства с параметром.

Если требуется все общие решения двух или нескольких неравенств, то решают систему неравенств. Как и систему уравнений, систему неравенств записывают с помощью фигурной скобки. Решение системы неравенств есть пересечение решений всех входящих в нее неравенств.

Одним из основных методов решения неравенств является метод интервалов.

Примеры решения неравенств

ПРИМЕР 1

Задание

Решить неравенство $x^{2} +3x+4>0$

Решение

Рассмотрим квадратное уравнение $x^{2} +3x+4=0$ и найдем его дискриминант

$D=3^{2} -4\cdot 1\cdot 4=-7<0$

Поскольку дискриминант отрицательный, то парабола 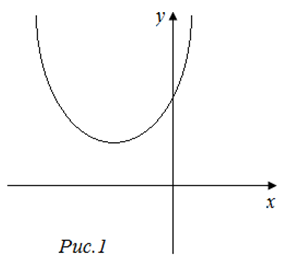$y=x^{2} +3x+4$ (рис. 1) лежит выше оси абсцисс и принимает только положительные значения, т.е. $x^{2} +3x+4>0$ при любых значения $x\in (-\infty ;+\infty )$ .

Ответ

$x\in (-\infty ;+\infty )$

ПРИМЕР 2

Задание

Решить неравенство

$\frac{x+3}{x-4} >0$

Решение

Дробь будет положительной в том случае, когда числитель и знаменатель одного знака, т.е. возможны два случая $\left\{\begin{array}{l} {x+3>0} \\ {x-4>0} \end{array}\right.$ или $\left\{\begin{array}{l} {x+3<0} \\ {x-4<0} \end{array}\right.$ . Таким образом, необходимо найти решение совокупности

$\left[\begin{array}{l} {\left\{\begin{array}{l} {x+3>0,} \\ {x-4>0,} \end{array}\right. } \\ {\left\{\begin{array}{l} {x+3<0,} \\ {x-4<0.} \end{array}\right. } \end{array}\right.$

Решим каждую систему неравенств отдельно:

1. $\left\{\begin{array}{l} {x+3>0} \\ {x-4>0} \end{array}\right. \Rightarrow \left\{\begin{array}{l} {x>-3} \\ {x>4} \end{array}\right. \Rightarrow x\in (4;+\infty )$ .

2. $\left\{\begin{array}{l} {x+3<0} \\ {x-4<0} \end{array}\right. \Rightarrow \left\{\begin{array}{l} {x<-3} \\ {x<4} \end{array}\right. \Rightarrow x\in (-\infty ;-3)$

Объединим полученные решения и запишем решение исходного неравенства $x\in (-\infty ;-3)\bigcup (4;+\infty )$ .

Ответ

$x\in (-\infty ;-3)\bigcup (4;+\infty )$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Решение неравенств

Определение и формулы неравенств

Основные правила, применяемые при решении неравенств

Примеры решения неравенств