Система неравенств и ее решение

Определение и формулы систем неравенств

ОПРЕДЕЛЕНИЕ

Если требуется найти общие решения двух или нескольких неравенств, то говорят, что нужно решить систему неравенств.

Как и систему уравнений, систему неравенств записывают с помощью фигурной скобки.

Решением системы неравенств называется значения переменных, превращающие каждое неравенство системы в верное числовое неравенство.

Все решения системы неравенств образуют множество решений системы неравенств. Если система решений не имеет, то говорят, что множеством ее решений является пустое множество: $x\in \emptyset$ .

Чтобы решить систему неравенств нужно найти пересечение множеств решений неравенств, составляющих систему, т.е. общие точки числовых промежутков.

Примеры решения систем неравенств

ПРИМЕР 1

Задание

Решите систему неравенств

$\left\{\begin{array}{l} {3x-1>-7,} \\ {3-4x>-9.} \end{array}\right$

Решение

Заданную систему можно преобразовать к виду

$\left\{\begin{array}{l} {3x>-6,} \\ {-4x>-12} \end{array}\right.$

или

$\left\{\begin{array}{l} {x>-2,} \\ {x<3.} \end{array}\right.$

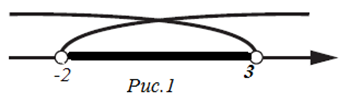
С помощью координатной прямой найдем пересечение множеств решений неравенств данной системы, т.е. пересечение промежутков $(-2;+\infty )$ и $(-\infty ;3)$ (рис. 1). Искомое пересечение состоит из чисел, удовлетворяющих неравенству $-2<x<3$ . Это множество является числовым промежутком $(-2;3)$ .

Ответ

$(-2;3)$

ПРИМЕР 2

Задание

Найти область определения функции

$y=\sqrt{3x+3} -\frac{1}{\sqrt{15-5x} }$

Решение

Искомая область определения — это множество решений системы

$\left\{\begin{array}{l} {3x+3\ge 0,} \\ {15-5x>0.} \end{array}\right$

Преобразуем эту систему к виду 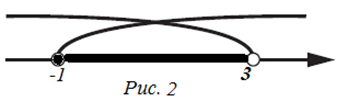$\left\{\begin{array}{l} {x\ge -1,} \\ {x<3.} \end{array}\right.$ Решением первого неравенства является числовой промежуток $[-1;+\infty )$ , а второго — $(-\infty ;3)$ . Пересечением этих промежутков является промежуток $[-1;3)$ (рис. 2)

Область определения при решении системы неравенств

Ответ

$[-1;3)$