Показательные неравенства и их решение
Определение и формулы показательных неравенств
При решении показательных неравенств используются те же методы, что и для показательных уравнений (приведение обоих частей неравенства к степени с одинаковыми основаниями либо введение новой переменной), а также правила решений простейших показательных неравенств вида ![]() или
или ![]() , где
, где ![]() .
.
Решая такие неравенства, используют монотонность показательной функции, а именно:
- Если
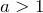 и
и 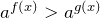 , то
, то 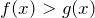 .
. - Если
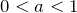 и
и 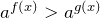 , то
, то 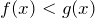 .
.
Примеры решения показательных неравенств
| Задание | Решить неравенство |
| Решение | Запишем правую и левую части неравенства в виде степени с основанием 5:
Поскольку или |
| Ответ |
| Задание | Решить неравенство |
| Решение | Введем замену Поскольку квадратичный трехчлен Учитывая условие Делаем обратную замену: Второе условие выполняется автоматически, поскольку |
| Ответ |











