Квадратные неравенства и их решение
Определение и формулы квадратных неравенств
Чтобы решить квадратное неравенство, нужно знать количество корней соответствующего квадратного уравнения ![]() . Сделать это можно с помощью дискриминанта: если дискриминант
. Сделать это можно с помощью дискриминанта: если дискриминант ![]() , то уравнение имеет два корня,
, то уравнение имеет два корня, ![]() — один корень,
— один корень, ![]() — действительных корней нет.
— действительных корней нет.
Знак старшего коэффициента ![]() определяет направление ветвей параболы
определяет направление ветвей параболы ![]() : если
: если ![]() , то ветви параболы направлены вверх, если
, то ветви параболы направлены вверх, если ![]() — вниз. В зависимости от знаков
— вниз. В зависимости от знаков ![]() и
и ![]() возможны такие варианты расположения параболы относительно оси абсцисс.
возможны такие варианты расположения параболы относительно оси абсцисс.
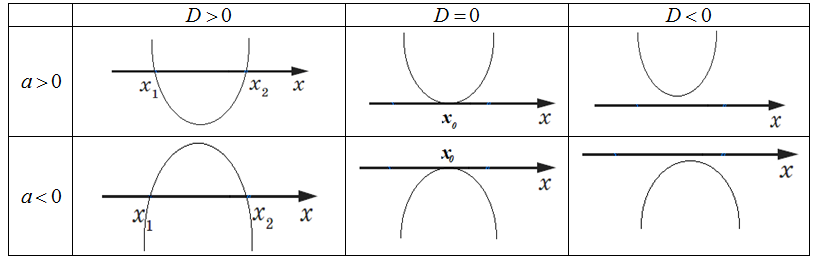
Решением неравенств ![]() (
(![]() ) будет числовой промежуток, на котором парабола лежит выше оси абсцисс.
) будет числовой промежуток, на котором парабола лежит выше оси абсцисс.
Решением неравенств ![]() (
(![]() ) будет числовой промежуток, на котором парабола лежит ниже оси абсцисс.
) будет числовой промежуток, на котором парабола лежит ниже оси абсцисс.
Если неравенство нестрогое, то концы промежутка включаются, если строгое, то не включаются.
Примеры решения квадратных неравенств
| Задание | Решить неравенство |
| Решение | Для квадратного трехчлена 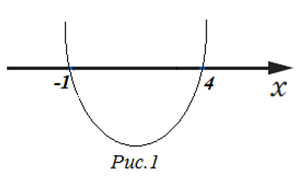
Схематически график функции |
| Ответ | |
| Задание | Решить неравенство |
| Решение | Для данного неравенства |
| Ответ |










