Метод интервалов решения неравенств

ОПРЕДЕЛЕНИЕ

Метод интервалов — это удобный и эффективный метод решения неравенств вида , где — рациональная функция (вместо знака «» может стоять любой из знаков «»)

Метод интервалов применяют при решении линейных, квадратных и дробно-рациональных неравенств.

Алгоритм метода интервалов

Метод интервалов решения неравенств основан на следующем алгоритме:

1. Решаем уравнение 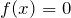и находим нули функции (если 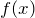— дробно-рациональная, то находим нули числителя и нули знаменателя).
2. Отмечаем полученные значения на числовой оси нули. Нули знаменателя всегда выколотые точки, нули числителя выколотые, если неравенство строгое; закрашенные, если неравенство нестрогое.
3. Полученные точки разбивают числовую ось на интервалы. В каждом интервале определяем знак функции .
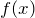4. Если при переходе через закрашенную точку знак не меняется, то эта точка (если она не находится внутри промежутка решения) является изолированной точкой-решением.

Примеры решения неравенств методом интервалов

ПРИМЕР 1

Задание	Решить неравенство
Решение	Сначала решим уравнение 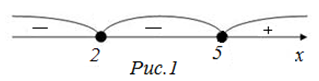. Корнями этого уравнения будут точки , а заданное неравенство можно записать в виде . Отмечаем точки на числовой оси. Поскольку неравенство нестрогое, то точки закрашенные. Определяем знак левой части неравенства на каждом промежутке. Для этого выбираем какое-либо значение, принадлежащее рассматриваемому интервалу, и подставляем его в левую часть неравенства вместо . Чтобы записать ответ, выбираем промежуток со знаком «+», а также не забываем точку 2, которая включается в решение (соответствующая ей точка закрашена), т.е. искомое решение .
Ответ

ПРИМЕР 2

Задание	Решить неравенство
Решение	Найдем нули числителя и знаменателя:     и     Отметим точки на числовой оси и определим знаки неравенства на каждом из промежутков Выбираем промежутки, на которых дробь положительна (то есть промежутки, помеченные знаком «+»), тогда .
Ответ