Неравенства с параметром и их решение
Определение и формулы неравенств с параметром
![]()
где ![]() — параметр,
— параметр, ![]() — переменная называется неравенством с параметром.
— переменная называется неравенством с параметром.
Чтобы решить неравенство с параметром нужно для всех значений параметра найти множество решений неравенства.
Неравенства с параметром в основном решаются следующим образом:
- Находится область допустимых значений параметра.
- ОДЗ параметра разбивается на интервалы, на которых неравенство решается одним и тем же способом.
- Отдельно на каждом интервале находится решение неравенства, зависящее от параметра.
- Решение неравенства записывается в виде перечисления интервалов изменения параметра с указанием для каждого из них решения исходного неравенства.
Эффективным также является графический метод решения неравенств с параметром.
Примеры решения неравенств с параметром
| Задание | Решить неравенство |
| Решение | Рассмотрим квадратный трехчлен В зависимости от знака дискриминанта функция 1. Множество решений исходного неравенства состоит из тех 2. 3. |
| Ответ | Если Если |
| Задание | Решить неравенство
|
| Решение | Рассмотрим функцию 1. Если 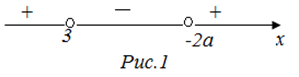
2. Если 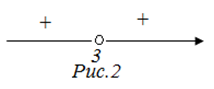
3. Если 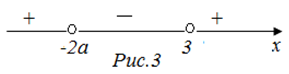
|
| Ответ | При |











