Наибольшее и наименьшее значение функции

Задача о нахождении наибольшего и наименьшего значения обычно решается для функции заданной и непрерывной на некотором отрезке.

ТЕОРЕМА

Если функция $f\left(x\right)$ непрерывна на отрезке $\left[a;\; b\right]$ , то среди её значений на этом отрезке есть наибольшее и наименьшее.

Правило отыскания наибольшего и наименьшего значения функции на отрезке. Чтобы найти наименьшее и наибольшее значения непрерывной функции $f\left(x\right)$ на отрезке $\left[a;\; b\right]$ , необходимо:

найти её значение на концах этого отрезка, то есть значения 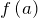$f\left(a\right)$ и $f\left(b\right)$ ;
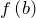найти её значение в стационарных точках функции, которые принадлежат отрезку $\left[a;\; b\right]$ ;
из всех найденных значений выбрать наибольшее и наименьшее.

Примеры нахождения наибольшего и наименьшего значения

ПРИМЕР 1

Задание

Найти наибольшее и наименьшее значение функции $y=\frac{x}{4} +\frac{1}{x}$ на отрезке $\left[1;\; 4\right]$

Решение

Найдем значение функции на концах заданного отрезка:

$y\left(1\right)=\frac{1}{4} +\frac{1}{1} =1\frac{1}{4} ;\ y\left(4\right)=\frac{4}{4} +\frac{1}{4} =1\frac{1}{4}$

Далее определим критические точки функции. Для этого вычислим и приравняем к нулю производную заданной функции

$y'=\frac{1}{4} -\frac{1}{x^{2} } ;$

$\frac{1}{4} -\frac{1}{x^{2} } =0 \Leftrightarrow \frac{x^{2} -4}{4x^{2} } =0 \Leftrightarrow \left[\begin{array}{l} {x\ne 0;} \\ {x^{2} -4=0;} \end{array}\right. \Leftrightarrow \left[\begin{array}{l} {x\ne 0;} \\ {\left(x-2\right)\left(x+2\right)=0} \end{array}\right. \Leftrightarrow$

$\Leftrightarrow \left[\begin{array}{l} {x\ne 0;} \\ {x_{1} =-2;\quad x_{2} =2;} \end{array}\right.$

Таким образом, $x_{1} =-2;\ x_{2} =2$ — стационарные точки заданной функции, из них только $x_{2} =2$ лежит на отрезке $\left[1;\; 4\right]$ . Найдем значение функции в этой точке

$y\left(2\right)=\frac{2}{4} +\frac{1}{2} =1$

Из трех значений $y\left(1\right)=1\frac{1}{4} ;\ y\left(4\right)=1\frac{1}{4} ;\ y\left(2\right)=\frac{2}{4} +\frac{1}{2} =1$ выбираем наибольшее и наименьшее.

Ответ

$y_{\mathop{\max }\limits_{\left[1;\; 4\right]} } =y\left(1\right)=y\left(4\right)=1\frac{1}{4} ;\ y_{\mathop{\min }\limits_{\left[1;\; 4\right]} } =y\left(2\right)=1$

ПРИМЕР 2

Задание

Найти наибольшее и наименьшее значение функции $y=\frac{x^{2} -x+1}{x^{2} +1}$ на отрезке $\left[-2;\; 2\right]$

Решение

Функция $y=\frac{x^{2} -x+1}{x^{2} +1}$ непрерывна на отрезке $\left[-2;\; 2\right]$ . Найдем её производную, используя правило дифференцирования частного

$y'=\frac{\left(x^{2} -x+1\right)^{{'} } \left(x^{2} +1\right)-\left(x^{2} -x+1\right)\left(x^{2} +1\right)^{{'} } }{\left(x^{2} +1\right)^{2} }=$

$=\frac{\left(2x-1\right)\left(x^{2} +1\right)-\left(x^{2} -x+1\right)\cdot 2x}{\left(x^{2} +1\right)^{2} } =\frac{x^{2} -1}{\left(x^{2} +1\right)^{2} }$

Приравнивая производную к нулю, получаем уравнение

$x^{2} -1=0 \Leftrightarrow \left(x-1\right)\left(x+1\right)=0 \Leftrightarrow x_{1} =-1; x_{2} =1$

Обе полученные точки принадлежат отрезку $\left[-2;\; 2\right]$ . Найдем значение функции на концах заданного отрезка и в критических точках и выберем из полученных значений наименьшее и наибольшее:

$y\left(-1\right)=\frac{\left(-1\right)^{2} -\left(-1\right)+1}{\left(-1\right)^{2} +1} =\frac{3}{2} ;\ y\left(1\right)=\frac{1^{2} -1+1}{1^{2} +1} =\frac{1}{2} ;$

$y\left(-2\right)=\frac{\left(-2\right)^{2} -\left(-2\right)+1}{\left(-2\right)^{2} +1} =\frac{7}{5} ;\ y\left(2\right)=\frac{2^{2} -2+1}{2^{2} +1} =\frac{3}{5}$

Значит, наименьшее значение функции на данном отрезке равно $\frac{1}{2}$ ; а наибольшее — числу $\frac{3}{2}$ .

Ответ

$y_{\mathop{\max }\limits_{\left[-2;\; 2\right]} } =y\left(-1\right)=\frac{3}{2} ;\ y_{\mathop{\min }\limits_{\left[-2;\; 2\right]} } =y\left(1\right)=\frac{1}{2}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Наибольшее и наименьшее значение функции

Примеры нахождения наибольшего и наименьшего значения