Монотонность функции. Возрастание и убывание

Возрастающая и убывающая функции в промежутке

ОПРЕДЕЛЕНИЕ

Функция называется возрастающей в промежутке $\left(a;\; b\right)$ , если большому значению аргумента соответствует большее значение функции, то есть для любой пары $x_{1} ,\; x_{2} \in \left(a,\; b\right)$ таких, что $x_{1} >\; x_{2}$ справедливо неравенство $f\left(x_{1} \right)>\; f\left(x_{2} \right).$

ОПРЕДЕЛЕНИЕ

Функция называется убывающей в промежутке $\left(a,\; b\right)$ , если большому значению аргумента соответствует меньшее значение функции, то есть для любой пары $x_{1} ,\; x_{2} \in \left(a,\; b\right)$ таких что $x_{1} >\; x_{2}$ справедливо $f\left(x_{1} \right)<\; f\left(x_{2} \right).$

Монотонная функция

ОПРЕДЕЛЕНИЕ

Функция называется монотонной на промежутке, если она на этом промежутке или возрастает, или убывает.

Достаточное условие монотонности функции.Пусть функция $f\left(x\right)$ определена и дифференцируема в промежутке $\left(a;\; b\right)$ . Для того чтобы функция была возрастающей в промежутке $\left(a;\; b\right)$ , достаточно, чтобы $f'\left(x\right)>0$ для всех $x\in \left(a,\; b\right)$

Для убывания функции достаточно, чтобы $f'\left(x\right)<0$ для всех $x\in \left(a,\; b\right).$

Для исследования функции $f\left(x\right)$ на монотонность необходимо:

найти её производную $f'\left(x\right)$ ;
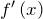найти критические точки функции как решения уравнения $f'\left(x\right)=0$ ;
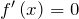определить знак производной на каждом из промежутков, на которые критические точки разбивают область определения функции;
согласно достаточному условию монотонности функции определить промежутки возрастания и убывания.

Примеры решения задач

ПРИМЕР 1

Задание

Найти промежутки монотонности функции $f\left(x\right)=3+9x^{2} -x^{3}$

Решение

Данная функция определена на всей числовой оси. Найдем производную заданной функции

$f'\left(x\right)=18x-3x^{2}$

Найдем критические точки, для этого решим уравнение

$18x-3x^{2} =0\Leftrightarrow 3x\left(6-x\right)=0\Leftrightarrow x_{1} =0; x_{2} =6$

Эти точки разбивают область определения на три интервала, занесем их в таблицу:

$x$	$\left(-\infty ;\; 0\right)$	$\left(0;\; 6\right)$	$\left(6;\; +\infty \right)$
$f'\left(x\right)$	—	+	—
$f\left(x\right)$	убывает	возрастает	убывает

Ответ

Функция $f\left(x\right)=3+9x^{2} -x^{3}$ возрастает на промежутке $\left(0;\; 6\right)$ и убывает на промежутках $\left(-\infty ;\; 0\right),\; \left(6;\; +\infty \right)$

ПРИМЕР 2

Задание

Определить промежутки возрастания и убывания функции

$y=\frac{x^{2} +1}{x}$

Решение

Область определения функции $D\left(y\right):x\in \left(-\infty ;\; 0\right)\bigcup \left(0;\; +\infty \right)$

Вычислим производную заданной функции

$y'=\frac{2x\cdot x-1\cdot \left(x^{2} +1\right)}{x} =\frac{x^{2} -1}{x}$

Приравняем найденную производную к нулю и найдем корни полученного уравнения

$\frac{x^{2} -1}{x} =0\Leftrightarrow \frac{\left(x+1\right)\left(x-1\right)}{x} =0 \Leftrightarrow x\ne 0; x_{1} =-1; x_{2} =1$

Получаем четыре интервала, внесем их в таблицу.

$x$	$\left(-\infty ;\; -1\right)$	$\left(-1;\; 0\right)$	$\left(0;\; 1\right)$	$\left(1;\; +\infty \right)$
$y'$	—	+	—	+
$y$	убывает	возрастает	убывает	возрастает

Ответ

Функция $y=\frac{x^{2} +1}{x}$ возрастает на промежутках $\left(-1;\; 0\right),\; \left(1;\; +\infty \right)$ и убывает на промежутках $\left(-\infty ;\; -1\right),\; \left(1;\; +\infty \right)$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Монотонность функции. Возрастание и убывание

Возрастающая и убывающая функции в промежутке

Монотонная функция

Примеры решения задач