График производной функции

С помощью графика производной функции $y = f'(x)$ можно определить точки экстремума и промежутки монотонности функции $y = f(x) .$ Для этого достаточно помнить, что:

функция 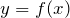$y = f(x)$ возрастает на промежутках, где производная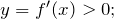 $y = f'(x) > 0 ;$
функция 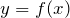$y = f(x)$ убывает на промежутках, где производная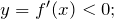 $y = f'(x) < 0 ;$
функция 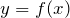$y = f(x)$ имеет критические точки, где производная 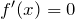$f'(x) = 0$ или не существует.
Замечание. Это верно только для внутренних точек области определения, точки на концах области определения не рассматриваются.
функция 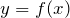$y = f(x)$ имеет точки экстремума там, где производная 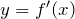$y = f'(x)$ меняет свой знак. В частности, функция $y = f(x)$ имеет точки максимума там, где производная меняет знак с плюса на минус; и точки минимума – там, где производная меняет знак с минуса на плюс.

Примеры работы с графиками производной

ПРИМЕР 1

Задание

На рисунке 1 изображен график производной функции 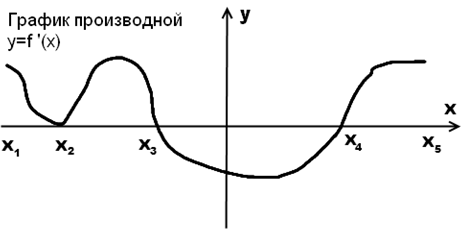$y = f'(x)$ . С помощью графика найти промежутки монотонности функции $y = f(x)$ , ее критические точки и точки экстремума.

Рисунок 1

Решение

Функция $y = f(x)$ возрастает на промежутках $(x_1 ; x_3)$ и $(x_4 ; x_5) ,$ так как на этих промежутках производная $y = f'(x)$ положительна (ее график расположен выше оси абсцисс). Точку $x_2$ не исключаем из промежутка возрастания, так как производная в этой точке равна нулю, но знак не меняет.

Функция $y = f(x)$ убывает на промежутке $(x_3 ; x_4) ,$ так как на этом интервале производная $y = f'(x)$ отрицательна (ее график расположен ниже оси $Ox$ ).

Критические точки функции $y = f(x)$ – это точки $x_2 , x_3 , x_4 .$ В этих точках производная обращается в нуль (график производной пересекает ось $Ox$ ). При этом точка $x = x_3$ является точкой максимума функции $y = f(x)$ , поскольку производная $y = f'(x)$ в этой точке меняет знак с плюса на минус (график производной пересекает абсцисс в направлении сверху вниз). Точка $x = x_4$ – точка минимума функции $y = f(x) ,$ так как производная $y = f'(x)$ в этой точке меняет знак с минуса на плюс (график производной пересекает $Ox$ в направлении снизу вверх).

То есть точками экстремума являются точки $x_3 , x_4 .$ В них производная не только обращается в нуль, но и меняет свой знак. Точка $x = x_2$ – критическая точка, не являющаяся точкой экстремума, поскольку производная $y = f'(x)$ не сменила знак.

Замечание. Таким образом, точками экстремума на графике производной являются те точки, в которых график не касается, а пересекает ось абсцисс.

По графику производной $y = f'(x)$ можно не только исследовать поведение функции $y = f(x)$ , но и попытаться схематически построить ее график. Поскольку для одной функции первообразных существует бесконечное множество, график функции по графику производной можно построить лишь схематично: точки экстремума и промежутки возрастания и убывания функции можно определить можно, а нули функции и экстремумы – нет.

ПРИМЕР 2

Задание

Дан график производной: 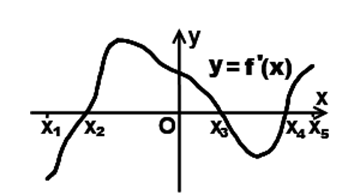$y = f'(x)$ (рис. 2). Построить график функции $y = f(x) .$

Рисунок 2

Решение

Точки $x_2 , x_3 , x_4 ,$ в которых производная $y = f'(x)$ обращается в нуль (график производной пересекает ось абсцисс) – это критические точки функции $y = f(x) .$ Так как в этих точках график функции $y = f'(x)$ пересекает ось абсцисс, то указанные точки являются точками экстремума функции $y = f(x)$ .

Так как в точках $x = x_2$ и $x = x_4$ производная меняет знак с «–» на «+», то эти точки являются точками минимума функции $y = f(x)$ . В точке $x = x_3$ производная меняет знак с «+» на «–», поэтому эта точка – точка максимума.

На промежутках $(x_1 ; x_2)$ и $(x_3 ; x_4)$ производная $f'(x) < 0$ (график функции лежит ниже оси абсцисс), следовательно, функция $y = f(x)$ на этих промежутках убывает. На промежутках $(x_2 ; x_3)$ и $(x_4 ; x_5)$ производная $f'(x) > 0$ (график функции лежит выше оси $Ox$ ), поэтому для функции $y = f(x)$ они являются промежутками возрастания.

Сказать что-то более определенное о нулях и других значениях функции $y = f(x)$ не получится.

Строим эскиз графика функции 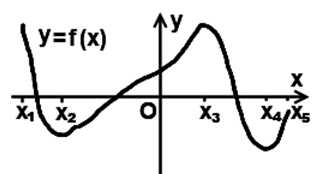$y = f(x)$ (рис. 3). Это один из множества графиков первообразных для функции $y = f'(x) .$ Другие могут быть получены из него параллельным переносом вдоль оси $Oy .$

Рисунок 3

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

График производной функции

Примеры работы с графиками производной