Область определения функции

ОПРЕДЕЛЕНИЕ

Областью определения или областью задания функции $y=f\left(x\right)$ называется множество значений $x$ , для которых существуют значения $y=f\left(x\right)$ .

Обозначается область определения функции — $D\left(f\right)$ или $D\left(y\right)$ .

Нахождение области определения функции

Схема нахождения области определения функций:

Если 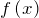$f\left(x\right)$ представляет собой многочлен, то областью определения функции 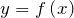$y=f\left(x\right)$ будет множество всех действительных чисел.
Если 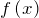$f\left(x\right)$ — рациональная дробь, то областью является множество всех действительных чисел кроме тех значений 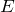$E$ , при которых знаменатель равен нулю.
Если функция имеет вид 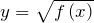$y=\sqrt{f\left(x\right)}$ , то областью определения будет множество решений неравенства $f\left(x\right)\ge 0$ .
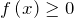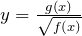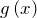Если функция имеет вид $y=\frac{g\left(x\right)}{\sqrt{f\left(x\right)}}$ , где $g\left(x\right)$ некоторый многочлен, то областью определения будет множество решений неравенства $f\left(x\right)>0$ .
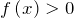Область определения суммы, разности или произведения двух или нескольких функций есть пересечение областей определений этих функций, для её отыскания составляется и затем решается система соответствующих условий.
Для логарифмической функции 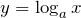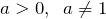$y=\log _{a} x$ ( $a>0,\; \; a\ne 1$ ) областью определения есть интервал $\left(0;\; +\infty \right)$ .

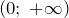Примеры решения задач

ПРИМЕР 1

Задание

Найти область определения следующих функций:

$1)\ y_{1} =x^{2} +2-\frac{3}{x-5} ;\ 2) \ y_{2} =\sqrt{x^{2} -3x+2} ;\ 3) \ y_{3} =\frac{2x-7}{\sqrt{3x+21} }$

Решение

1) Функцию $y_{1} =x^{2} +2-\frac{3}{x-5}$ можно представить в виде разности двух функций

$f_{1} \left(x\right)=x^{2} +2;\ f_{2} \left(x\right)=\frac{3}{x-5}$

Функция $f_{1} \left(x\right)$ является многочленом и её областью определения есть множество всех действительных чисел $R$ .

Функция $f_{2} \left(x\right)$ является дробно-рациональной. Найдем значения $x$ , которые обнуляют знаменатель

$x-5\ne 0\Rightarrow x\ne 5$

Таким образом, область определения функции $y_{1}$ находится из системы

$\left\{\begin{array}{c} {x\in R,} \\ {x\ne 5,} \end{array}\right. \quad \Rightarrow \quad D\left(y_{1} \right):x\in \left(-\infty ,\; 5\right)\bigcup \left(5,\; +\infty \right)$

2) Для нахождения области определения $y_{2} =\sqrt{x^{2} -3x+2}$ решим неравенство

$x^{2} -3x+2\ge 0$

Разложим на множители левую часть этого неравенства. Для этого решим уравнение $x^{2} -3x+2=0$ . По теореме Виета: $x_{1} +x_{2} =3;\ x_{1} \cdot x_{2} =2$ , отсюда $x_{1} =1,\ x_{2} =2$ . Таким образом, неравенство примет вид

$\left(x-1\right)\left(x-2\right)\ge 0$

Обозначим найденные корни на числовой оси и определим знак неравенства на полученных интервалах.

Таким образом, $D\left(y_{2} \right):x\in \left(\left. -\infty ,\; 1\right]\right. \bigcup \left[\left. 2,\; +\infty \right)\right.$ .

3) Функция $y_{3} =\frac{2x-7}{\sqrt{3x+21} }$ представляет собой дробно-рациональную функцию, в числителе которой многочлен. Область определения многочлена есть множество действительных чисел $R$ . В знаменателе корень, область его определения находим из системы

$\left\{\begin{array}{c} {3x+21\ge 0,} \\ {3x+21\ne 0,} \end{array}\right. \Rightarrow 3x+21>0\Rightarrow 3x>-21\Rightarrow x>-7$

Таким образом, $D\left(y_{3} \right):x\in \left(-7,\; +\infty \right)$ .

Ответ

$D\left(y_{1} \right):x\in \left(-\infty ,\; 5\right)\bigcup \left(5,\; +\infty \right),$

$D\left(y_{2} \right):x\in \left(\left. -\infty ,\; 1\right]\right. \bigcup \left[\left. 2,\; +\infty \right)\right ,$

$D\left(y_{3} \right):x\in \left(-7,\; +\infty \right)$

ПРИМЕР 2

Задание

Найти область определения следующих функций:

$1)\ y_{1} =\sqrt{3^{2x-5} -1} ;\ 2)\ y_{2} =\sqrt{-\log _{2} x+1} ;\ 3)\ y_{3} =\log _{x} \left(x-0,5\right)$

Решение

1) Для нахождения области определения функции $y_{1} =\sqrt{3^{2x-5} -1}$ решим неравенство

$3^{2x-5} -1>0\Rightarrow 3^{2x-5} >1\Rightarrow 3^{2x-5} >3^{0}$

Поскольку основание степени $3>1$ , то приходим к неравенству

$2x-5>0\Rightarrow 2x>5\Rightarrow x>2,5$

Таким образом, $D\left(y_{1} \right):x\in \left(2,5;\; +\infty \right)$ .

2) Для нахождения области определения функции $y_{2} =\sqrt{-\log _{2} x+1}$ нужно учесть, что подкоренное выражение должно быть неотрицательным, а подлогарифмическая функция — положительной. Имеет место система неравенств

$\left\{\begin{array}{l} {-\log _{2} x+1\ge 0,} \\ {x>0.} \end{array}\right.$

Решим первое неравенство отдельно

$-\log _{2} x+1\ge 0\Rightarrow \log _{2} x\le 1$

Согласно определению логарифма, придем к неравенству

$x\le 2$

Возвращаясь к системе неравенств, имеем

$\left\{\begin{array}{l} {x\le 2,} \\ {x>0,} \end{array}\right. \quad \Rightarrow \quad 0<x\le 2$

Таким образом, искомая область определения $D\left(y_{2} \right):x\in \left(\left. 0,\; 2\right]\right.$ .

3) Учитывая определение логарифмической функции, область определения $y_{3} =\log _{x} \left(x-0,5\right)$ найдем из системы

$\left\{\begin{array}{l} {x>0,} \\ {x\ne 1,} \\ {x-0,5>0,} \end{array}\right. \quad \Rightarrow \quad \left\{\begin{array}{l} {x>0,} \\ {x\ne 1,} \\ {x>0,5;} \end{array}\right. \quad \Rightarrow \quad \left\{\begin{array}{l} {x\ne 1,} \\ {x>0,5;} \end{array}\right. \Rightarrow \left(0,5;\; 1\right)\bigcup \left(1;+\infty \right)$

В результате имеем, что $D\left(y_{3} \right):x\in \left(0,5;\; 1\right)\bigcup \left(1;\, +\infty \right)$ .

Ответ

$D\left(y_{1} \right):x\in \left(2,5;\; +\infty \right);$

$D\left(y_{2} \right):x\in \left(\left. 0,\; 2\right]\right;$

$D\left(y_{3} \right):x\in \left(0,5;\; 1\right)\bigcup \left(1;\, +\infty \right)$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Область определения функции

Нахождение области определения функции

Примеры решения задач