Четность и нечетность функции

Определения и свойства четных и нечетных функций

ОПРЕДЕЛЕНИЕ

Функция $f\left(x\right)$ называется четной функцией, если для любого $x$ из области определения выполняется равенство $f\left(-x\right)=f\left(x\right).$

Функция $f\left(x\right)$ называется нечетной функцией, если для любого $x$ из области определения выполняется равенство $f\left(-x\right)=-f\left(x\right)$ .

Если ни одно из условий $f\left(-x\right)=f\left(x\right)$ или $f\left(-x\right)=-f\left(x\right)$ не выполняется, то говорят, что функция $f\left(x\right)$ не является ни четной, ни нечетной (или функцией общего вида)

График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.

При исследовании функции на четность и нечетность можно использовать следующие свойства:

Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.
Произведение двух четных функций является четной функцией, равно как и произведение двух нечетных функций. Произведение четной и нечетной функции — нечетная функция.
Если функция 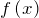$f\left(x\right)$ четная (нечетная), то и функция 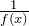$\frac{1}{f\left(x\right)}$ четная (нечетная).

Примеры решения задач

ПРИМЕР 1

Задание

Используя определение исследовать на четность и нечетность следующие функции

$1)\ f_{1} \left(x\right)=2x^{4} -3x^{2} +6;\ 2)\ f_{2} \left(x\right)=8x^{3} -7x;\ 3)\ f_{3} \left(x\right)=x^{4} -4x+5$

Решение

1) Рассмотрим значение функции $f_{1} \left(x\right)=2x^{4} -3x^{2} +6$ в точке $\left(-x\right)$ :

$f_{1} \left(-x\right)=2\cdot \left(-x\right)^{4} -3\cdot \left(-x\right)^{2} +6=2x^{4} -3x^{2} +6=f_{1} \left(x\right)$

Для заданной функции выполняется условие $f_{1} \left(-x\right)=f_{1} \left(x\right)$ , следовательно, она четная.

2) Найдем значение функции $f_{2} \left(x\right)=8x^{3} -7x$ в точке $\left(-x\right)$ :

$f_{2} \left(-x\right)=8\cdot \left(-x\right)^{3} -7\cdot \left(-x\right)=-8x^{3} +7x=-\left(8x^{3} -7x\right)=-f_{2} \left(x\right)$

Для этой функции выполняется условие $f_{2} \left(-x\right)=-f_{2} \left(x\right)$ , следовательно, она является нечетной.

3) Найдем значение функции $f_{3} \left(x\right)=x^{4} -4x+5$ в точке $\left(-x\right)$ :

$f_{3} \left(-x\right)=\left(-x\right)^{4} -4\cdot \left(-x\right)+5=x^{4} +4x+5$

Таким образом, $f_{3} \left(-x\right)\ne f_{3} \left(x\right);\ f_{3} \left(-x\right)\ne -f_{3} \left(x\right)$ , значит, функция $f_{3} \left(x\right)=x^{4} -4x+5$ не является ни четной, ни нечетной.

Ответ

1) $f_{1} \left(x\right)=2x^{4} -3x^{2} +6$ — четная;

2) $f_{2} \left(x\right)=8x^{3} -7x$ — нечетная;

3) $f_{3} \left(x\right)=x^{4} -4x+5$ — ни четная, ни нечетная.

ПРИМЕР 2

Задание

Исследовать функцию $f\left(x\right)=\frac{x^{2} +4}{3x^{6} +x^{4} +7}$ на четность, используя свойства четных и нечетных функций.

Решение

Исследуем отдельно четность функции, которые находятся в числителе и знаменателе:

$g\left(-x\right)=\left(-x\right)^{2} +4=x^{2} +4=g\left(x\right)$

то есть функция $g\left(x\right)$ четная; аналогично

$h\, \left(-x\right)=3\left(-x\right)^{6} +\left(-x\right)^{4} +7=3x^{6} +x^{4} +7=h\, \left(x\right),$

а тогда и функция $h\left(x\right)$ четная.

По свойству 3, так как $h\, \left(x\right)$ — четная, то четной будет и функция $\frac{1}{h\, \left(x\right)} =\frac{1}{3x^{6} +x^{4} +7}$ . Тогда исходную функцию $f\left(x\right)$ можно представить в виде произведения четных функций $f\left(x\right)=g\left(x\right)\cdot \frac{1}{h\, \left(x\right)}$ , следовательно, по свойству 2, $f\left(x\right)$ — четная.

Ответ

Исследованная функция четная.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Четность и нечетность функции

Определения и свойства четных и нечетных функций

Примеры решения задач