Свойства функции

ОПРЕДЕЛЕНИЕ

Функцией $y=f(x)$ называется правило, по которому каждому значению переменной $x$ ставится в соответствие значение переменной $y$ .

Переменная $x$ является независимой переменной (ее называют «аргумент»), а переменная $y$ – зависимая переменная («функция»).

Значения, которые может принимать независимая переменная $x$ , образуют область определения функции (обозначают $D(f)$ ), а значения переменной $y$ образуют область значений функции (обозначают $E(f)$ ).

Существует несколько способов задания функции – аналитический, табличный, графический.

ОПРЕДЕЛЕНИЕ

Графиком функции называется множество точек плоскости с координатами $(x,f(x))$ . Для построения графика функцию нужно исследовать, а для этого необходимо знать свойства функции.

Основные свойства функции

1.Четность и нечетность функции.

Функция $f(x)$ называется четной, если ее область определения симметрична относительно нуля и для любого $x$ из области определения функции

$f(-x)=f(x)$

График четной функции симметричен относительно оси $Oy$ .

Функция $f(x)$ называется нечетной, если ее область определения симметрична относительно нуля и для любого $x$ из области определения функции

$f(-x)=-f(x)$

График четной функции симметричен относительно начала координат.

Если не выполняется ни одно из условий $f(-x)=f(x),\ f(-x)=-f(x)$ , то функция называется ни четной, ни нечетной (или функцией общего вида).

ПРИМЕР

Задание

Исследовать функцию $f(x)={{x}^{2}}$ на четность.

Решение

Для заданной функции

$f(-x)={{(-x)}^{2}}={{x}^{2}}=f\left( x \right)$

Значит, эта функция четная.

Ответ

Функция четная.

2. Периодичность функции.

Функция называется периодической, если существует такое ненулевое число $T$ , что $f(x)=f(x+T)$ для любого $x$ из области определения функции.

ПРИМЕР

Функция $f\left( x \right)=\sin x$ является периодической, так как

$f\left( x+2\pi \right)=\sin (x+2\pi )=\sin x$

Период этой функции $T=2\pi$ .

Заметим, что все тригонометрические функции являются периодическими.

3. Монотонность (возрастание, убывание) функции.

Функция называется возрастающей на некотором промежутке, если для любых ${{x}_{1}},{{x}_{2}}$ из этого промежутка таких, что ${{x}_{1}}>{{x}_{2}}$ , выполняется неравенство

$f({{x}_{1}})>f({{x}_{2}})$

Функция называется убывающей на некотором промежутке, если для любых ${{x}_{1}},{{x}_{2}}$ из этого промежутка таких, что ${{x}_{1}}<{{x}_{2}}$ выполняется

$f({{x}_{1}})>f({{x}_{2}})$

4. Экстремумы функции.

Точка ${{x}_{0}}$ называется точкой максимума функции $f(x)$ , если для всех $x$ из некоторой окрестности этой точки, выполнено $f({{x}_{0}})>f(x)$ . Значение ${{y}_{0}}=f({{x}_{0}})$ называется максимумом этой функции.

Точка ${{x}_{0}}$ называется точкой минимума функции $f(x)$ , если для всех $x$ из некоторой окрестности, выполнено $f({{x}_{0}})<f(x)$ . Значение ${{y}_{0}}=f({{x}_{0}})$ называется минимумом этой функции.

Чтобы исследовать функцию $f(x)$ на экстремум необходимо:

Найти производную ${f}'(x)$ .
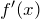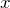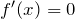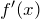Найти значения $x$ , в которых ${f}'(x)=0$ или ${f}'(x)$ не существует (найти критические точки).
Исследовать знак производной слева и справа от каждой критической точки.
Найти значение функции в экстремальных точках.

5. Нули функции.

Нуль функции – это такое значение аргумента ${{x}_{0}}$ , при котором значение функции $f({{x}_{0}})$ равно нулю.

ПРИМЕР 1

Задание

Исследовать функцию $f(x)={{x}^{4}}+2\cos 3x+{{x}^{2}}-5$ на четность/нечетность.

Решение

Найдем значение функции $f(-x)$ :

$f(-x)={{(-x)}^{4}}+2\cos (-3x)+{{(-x)}^{2}}-5={{x}^{4}}+2\cos 3x+{{x}^{2}}-5=f(x)$

Так как $f(-x)=f(x)$ , то функция является четной.

Ответ

Функция четная.

ПРИМЕР 2

Задание

Исследовать функцию $f(x)={{x}^{2}}+6x-5$ на экстремум.

Решение

Найдем производную функции и приравняем ее к нулю:

${f}'(x)=2x+6=0\Rightarrow x=-3$

Производная функции определена во всех точках, следовательно, имеем одну критическую точку 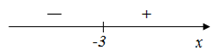$x=-3$ . Отметим ее на числовой прямой и определим знак производной справа и слева от нее

При переходе через точку $x=-3$ производная сменила свой знак с «–» на «+», значит в этой точке функция достигает минимума. Найдем значение функции в этой точке:

$f(-3)={{(-3)}^{2}}+6\cdot (-3)-5=-14$

Точка с координатами $(-3,-14)$ является точкой минимума.

Ответ

Точка $(-3,-14)$ – точка минимума.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Свойства функции

Основные свойства функции