Промежутки выпуклости и вогнутости функции

ОПРЕДЕЛЕНИЕ

Функция $y=f\left(x\right)$ называется выпуклой (вогнутой) на некотором интервале $\left(a;\; b\right)$ , если на этом интервале график $y=f\left(x\right)$ расположен не выше (не ниже) касательной, проведённой к нему в произвольной точке интервала $\left(a;\; b\right)$ .

Условия вогнутости и выпуклости функции на интервале

Если на некотором интервале $\left(a;\; b\right)$ вторая производная функции $y=f\left(x\right)$ сохраняет знак «+» для всех точек интервала, то на этом интервале функция вогнута (обозначается $\bigcup$ ). Если на некотором интервале $\left(a;\; b\right)$ вторая производная $f''\left(x\right)<0$ для всех точек интервала, то на этом говорят, что функция выпукла (обозначается $\bigcap$ ).

Для промежутков вогнутости и выпуклости функции $f\left(x\right)$ необходимо:

найти область определения функции;
найти её вторую производную $f''\left(x\right)$ ;
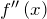найти стационарные точки функции, то есть решить уравнение $f''\left(x\right)=0$ ;
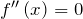определить знак второй производной на каждом из промежутков, на которые стационарные точки разбивают область определения функции;
согласно условию вогнутости и выпуклости функции на интервале определить промежутки вогнутости и выпуклости.

Примеры решения задач

ПРИМЕР 1

Задание

Найти промежутки вогнутости и выпуклости функции $y=\left(x^{2} -2\right)^{2}$

Решение

Данная функция определена на всей числовой оси. Найдем вторую производную заданной функции

$y'=2\left(x^{2} -2\right)\cdot 2x=4x^{3} -8x;$

$y''=12x^{2} -8$

Приравняем к нулю вторую производную и найдем корни полученного уравнения

$12x^{2} -8=0 \Leftrightarrow 3x^{2} -2=0 \Leftrightarrow x_{1,2} =\pm \sqrt{\frac{2}{3} }$

Полученные точки разбивают область определения на три интервала. Определим в этих интервалах знак второй производной и результаты занесем в таблицу

$x$	$\left(-\infty ;-\sqrt{\frac{2}{3} } \right)$	$\left(-\sqrt{\frac{2}{3} } ;\sqrt{\frac{2}{3} } \right)$	$\left(\sqrt{\frac{2}{3} } ;+\infty \right)$
$y''$	$+$	—	+
$y$	$\bigcup$	$\bigcap$	$\bigcup$

Ответ

Функция $y=\left(x^{2} -2\right)^{2}$ выпукла на интервале $\left(-\sqrt{\frac{2}{3} } ;\sqrt{\frac{2}{3} } \right)$ и вогнута на промежутках $\left(-\infty ;-\sqrt{\frac{2}{3} } \right),\; \left(\sqrt{\frac{2}{3} } ;+\infty \right)$

ПРИМЕР 2

Задание

Найти промежутки вогнутости и выпуклости функции

$y=\frac{2x}{x^{2} +1}$

Решение

Область определения функции: $D(y):\, x\in \left(-\infty ;\; +\infty \right)$ . Найдем вторую производную функции

$y'=\frac{2\left(x^{2} +1\right)-2x\cdot 2x}{\left(x^{2} +1\right)^{2} } =\frac{2x^{2} +2-4x^{2} }{\left(x^{2} +1\right)^{2} } =\frac{-2\left(x^{2} -1\right)}{\left(x^{2} +1\right)^{2} } ;$

$y''=-2\cdot \frac{2x\cdot \left(x^{2} +1\right)^{2} -2\left(x^{2} +1\right)\cdot 2x\cdot \left(x^{2} -1\right)}{\left(x^{2} +1\right)^{4} } =-2\cdot \frac{2x\cdot \left(x^{2} +1\right)-4x\cdot \left(x^{2} -1\right)}{\left(x^{2} +1\right)^{3} } =$

$=\frac{-4x\cdot \left(x^{2} +1-2x^{2} +2\right)}{\left(x^{2} +1\right)^{3} } =\frac{4x\cdot \left(x^{2} -3\right)}{\left(x^{2} +1\right)^{3} }$

Найдем решения уравнения $y''=0$ (стационарные точки функции):

$\frac{4x\cdot \left(x^{2} -3\right)}{\left(x^{2} +1\right)^{3} } =0 \Leftrightarrow x\cdot \left(x^{2} -3\right)=0 \Leftrightarrow x_{1} =0, x_{2,3} =\pm \sqrt{3}$

Эти точки разбивают область определения на четыре интервала. Определим в этих интервалах знак второй производной и составим в таблицу

$x$	$\left(-\infty ;\; -\sqrt{3} \right)$	$\left(-\sqrt{3} ;0\right)$	$\left(0;\; \sqrt{3} \right)$	$\left(\sqrt{3} ;+\infty \right)$
$y''$	—	+	—	+
$y$	$\bigcap$	$\bigcup$	$\bigcap$	$\bigcup$

Ответ

Функция выпукла на промежутках $\left(-\infty ;\; -\sqrt{3} \right),\ \left(0;\; \sqrt{3} \right)$ и вогнута на промежутках $\left(-\sqrt{3} ;0\right),\ \left(\sqrt{3} ;+\infty \right)$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Промежутки выпуклости и вогнутости функции

Условия вогнутости и выпуклости функции на интервале

Примеры решения задач