Парабола
Определение параболы
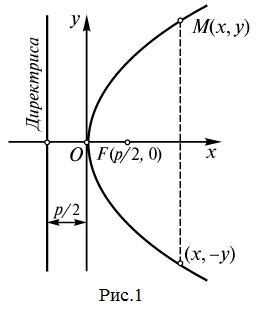
Точка ![]() называется фокусом параболы, а фиксированной прямая – директрисой параболы.
называется фокусом параболы, а фиксированной прямая – директрисой параболы.
Основные формулы и определения параболы
Уравнение директрисы параболы
![]()
Каноническое уравнение параболы имеет вид
![]()
где ![]() – расстояние от фокуса до директрисы параболы и называется фокальным параметром параболы.
– расстояние от фокуса до директрисы параболы и называется фокальным параметром параболы.
Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы (на рисунке 1 это точка F).
Если парабола задана своим каноническим уравнением, то осью параболы является ось ![]() , а вершиной параболы – начало координат.
, а вершиной параболы – начало координат.
Хорды, проходящие через фокус параболы, называются ее фокальными хордами.
Пусть точка ![]() лежит на параболе. Касательная к параболе в этой точке определяется уравнением:
лежит на параболе. Касательная к параболе в этой точке определяется уравнением:
![]()
Примеры решения задач
| Задание | Составить каноническое уравнение параболы, если расстояние от фокуса до директрисы равно 12. |
| Решение | Каноническое уравнение параболы имеет вид
где |
| Ответ | Каноническое уравнение параболы: |
| Задание | Найти координаты фокуса и составить уравнение директрисы параболы |
| Решение | У заданной параболы |
| Ответ |











