Свойства параболы
Парабола является графиком квадратичной функции, которая задается уравнением
![]()
и обладает следующими свойствами:
– если коэффициент ![]() и вершина параболы имеет координаты
и вершина параболы имеет координаты ![]() , то
, то
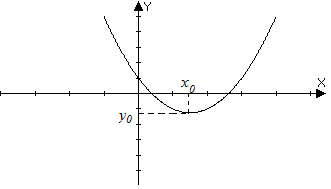
Область значений – ![]() .
.
Функция убывает при ![]() , возрастает при
, возрастает при ![]() .
.
Функция непрерывна и выпукла вниз.
Минимум функции ![]() .
.
– если коэффициент a<0, а вершина параболы имеет координаты ![]() , то
, то
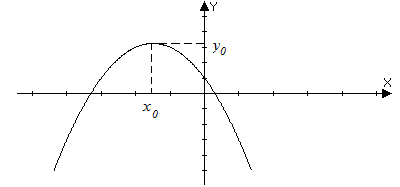
Область определения – ![]() .
.
Область значений – ![]() .
.
Функция убывает при ![]() , возрастает при
, возрастает при ![]() .
.
Функция непрерывна и выпукла вверх.
Максимум функции ![]() .
.
Примеры решения задач
| Задание | По графику функции, изображенной на рисунке 1, найти промежутки убывания и возрастания функции.
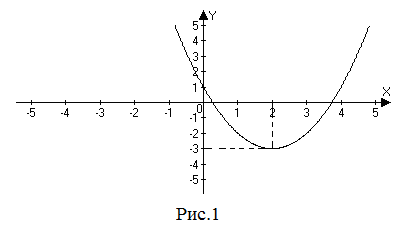
|
| Решение | На графике изображена парабола с вершиной в точке |
| Ответ | Функция убывает при |
| Задание | Найти максимальное значение функции |
| Решение | Графиком функции Следовательно, максимальное значение функции |
| Ответ | Максимальное значение функции: |











