Уравнение Эйнштейна для фотоэффекта

Определение фотоэффекта

ОПРЕДЕЛЕНИЕ

Суть фотоэффекта состоит в способности атомов к ионизации под действием света.

Если атомы подвергнуть облучению светом, то свет будет поглощаться атомами. Естественно допустить, что при определённых условиях поглощение будет столь велико, что внешние (валентные) электроны будут отрываться от атомов. Это явление наблюдается в действительности. Классическая электродинамика, обычная волновая теория света не в состоянии дать удовлетворительное объяснение фотоэффекту. Эйнштейн выдвигает предположение, что свет сам по себе имеет корпускулярную природу, что имеет смысл смотреть на свет не как на поток волн, а как на поток частиц. Свет не только излучается, но и распространяется и поглощается в виде квантов! Эти кванты, или частицы, световой энергии Эйнштейн назвал фотонами.

Фотоны, падая на поверхность металла, проникают на очень короткое расстояние в металл и поглощаются нацело отдельными его электронами проводимости. Они сразу же увеличивают свою энергию до значения, достаточного, чтобы преодолеть потенциальный барьер вблизи поверхности металла, и вылетают наружу.

Уравнение Эйнштейна для фотоэффекта

Из закона сохранения энергии следует уравнение Эйнштейна для внешнего фотоэффекта, вызываемого монохроматическим светом:

$h\nu =A+\frac{mv^2_{max}}{2}$

где $h\nu$ – энергия фотона, $m$ — масса электрона, $A$ — работа выхода электрона.

Данное уравнение означает, что энергия фотона после поглощения его, с одной стороны, расходуется на преодоление потенциального барьера (эта часть энергии называется работой выхода электрона из металла), а с другой стороны, частично сохраняется у электрона вне металла в виде кинетической энергии. Это соотношение подтверждает тот факт, что энергия фотоэлектронов, действительно, никак не зависит от интенсивности света, а линейно зависит от частоты света. Уравнение Эйнштейна позволяет измерить постоянную Планка h.

Из уравнения Эйнштейна следует существование красной границы фотоэффекта.

При достаточно низкой частоте света фотоэффект не наблюдается: энергии фотона не хватает на преодоление потенциального барьера. Та критическая частота, при которой прекращается фотоэффект, называется красной границей фотоэффекта. Красная граница фотоэффекта определяется работой выхода:

$h{\nu }_{kr}=A$

У различных металлов красная граница фотоэффекта различна

Примеры решения задач

ПРИМЕР 1

Задание

Для определения постоянной Планка была составлена цепь (рис. 1). Когда скользящий контакт потенциометра находится в крайнем левом положении, чувствительный амперметр при освещении фотоэлемента регистрирует слабый фототок. Передвигая скользящий контакт вправо, постепенно увеличивают запирающее напряжение до тех пор, пока в цепи прекратится фототок. При освещении фотоэлемента фиолетовым светом с частотой 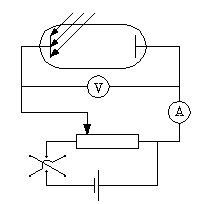${\nu }_2=750$ ТГц запирающее напряжение 2 В, а при освещении красным светом ${\nu }_1$ =390 TГц запирающее напряжение равно 0,5 В. Какое значение постоянной Планка было получено?

Пример 1, Уравнение Эйнштейна для фотоэффекта

рис. 1

Решение

В качестве основы для решения задачи служит уравнение Эйнштейна: $h\nu =A+\frac{mv^2}{2}$

В том случае когда достигают напряжения при котором фототок прекращается отрицательная работа внешнего поля над электронами ровна кинетической энергии электрона, то есть:

$eU_z=\frac{mv^2}{2}$

Тогда уравнение Эйнштейна примет вид:

$h\nu =A+eU_z$ Запишем это уравнение для двух состояний, описанных в условиях задачи:

1. $h{\nu }_1=A+eU_{z1}$

2. $h{\nu }_2=A+eU_{z2}$

Вычтем первое уравнение из второго, получим:

$h({\nu }_2-{\nu }_1)=e(U_{z2}-U_{z1}),\ h=\frac{e(U_{z2}-U_{z1})}{({\nu }_2-{\nu }_1)}$

Дополним данные задачи табличным значением заряда электрона $e=1,6\cdot {10}^{-19}$ Кл

Переведем данные в СИ:

${\nu }_2$ =750 TГц = $750\cdot 10^{12}$ Гц,

${\nu }_1$ =390 TГц = $390 \cdot 10^{12}$ Гц

Проведем расчёт

$h=\frac{1,6 \cdot 10^{-19}(2-0,5)}{(7,5-3,9)10^{14}} =6,67\cdot 10^{-34}$ Дж•с

Ответ

Постоянная Планка равна $6,67\cdot 10^{-34}$ Дж•с.

ПРИМЕР 2

Задание

В вакуумном фотоэлементе, облучаемом светом с частотой $\nu$ , фотоэлектрон попадает в задерживающее электрическое поле. К электродам фотоэлемента приложено напряжение U, расстояние между электродами равно H, электрон вылетает под углом $30^{\circ}$ к плоскости катода. Как изменяется импульс и координаты электрона по сравнению с начальными в момент его возврата на катод? А- работа выхода.

Решение

При решении задачи используем уравнение Эйнштейна для фотоэффекта:

$h\nu =A+\frac{mv^2_0}{2}$

Далее надо представить движение электрона. Допустим, что в области движения электрона электрическое поле однородно. Такое допущение можно сделать, если считать, что анод располагается сравнительно далеко от вершины траектории электрона. Найдем изменение импульса электрона по возвращении на катод. Выполним построения рис. 2.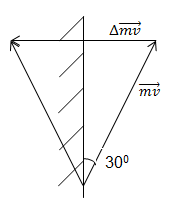

Пример 2, Уравнение Эйнштейна для фотоэффекта

рис. 2

Изменение импульса- основание треугольника с углом при вершине $60^{\circ}$ . Тогда $\left|\Delta m\overrightarrow{v}\right|=mv_0$ ,

$v_0=\sqrt{2m(h\nu -A)}$ , тогда $\Delta p=m\sqrt{2m(h\nu -A)}$ .

Найдем на катоде место возврата электрона. Движение электрона отклоняется от нормали к плоскости катода. Этот сдвиг осуществляется с постоянной скоростью, равной $v_0{ \cos {30}^{\circ}.\ }$

В однородном поле электрон летит с постоянным ускорением, равным eU/Hm. Время движения находим из соотношения:

$\tau =\frac{2v_0{ \cos {30}^{\circ}}}{\frac{eU}{Hm}}=\frac{2Hmv_0{ \cos {30}^{\circ}}}{eU}$

С учетом выражений, полученных для $v_0$ и $\tau$ величину отклонения электрона от начального положения на катоде определим из выражения

$\Delta x=v_0{ \cos {30}^{\circ}\cdot \tau =\frac{2Hmv^2_0{{ \cos }^2 {30}^{\circ}}}{eU}=\frac{3Hm^2(h\nu -A)}{eU}}$

Ответ

Изменение импульса электрона $\Delta p=m\sqrt{2m(h\nu -A)}$ , изменение координаты $\Delta x=\frac{3Hm^2(h\nu -A)}{eU}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Уравнение Эйнштейна для фотоэффекта

Определение фотоэффекта

Уравнение Эйнштейна для фотоэффекта

Примеры решения задач