Уравнение Пуассона
Определение и формула уравнения Пуассона
Уравнение Пуассона имеет вид:
![]()
Здесь ![]() – объем, занимаемый газом,
– объем, занимаемый газом, ![]() – его давление, а величина
– его давление, а величина ![]() называется показателем адиабаты.
называется показателем адиабаты.
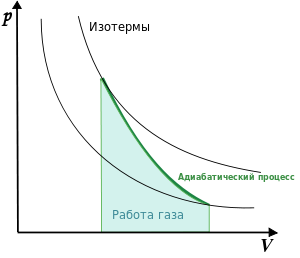
Показатель адиабаты в уравнении Пуассона
Показатель адиабаты можно рассчитать, как отношение изобарной теплоемкости газа к его изохорной теплоемкости:
![]()
В практических расчётах удобно помнить, что для идеального газа показатель адиабаты равен ![]() , для двухатомного –
, для двухатомного – ![]() , а для трёхатомного –
, а для трёхатомного – ![]() .
.
Как же быть с реальными газами, когда важную роль начинают играть силы взаимодействия между молекулами? В этом случае показатель адиабаты для каждого исследуемого газа можно получить экспериментально. Один из таких методов был предложен в 1819 году Клеманом и Дезормом. Мы наполняем баллон холодным газом, пока давление в нём не достигнет ![]() . Затем открываем кран, газ начинает адиабатически расширяться, а давление в баллоне падает до атмосферного
. Затем открываем кран, газ начинает адиабатически расширяться, а давление в баллоне падает до атмосферного ![]() . После того, как газ изохорно прогреется до температуры окружающей среды, давление в баллоне повысится до
. После того, как газ изохорно прогреется до температуры окружающей среды, давление в баллоне повысится до ![]() . Тогда показатель адиабаты можно рассчитать за формулой:
. Тогда показатель адиабаты можно рассчитать за формулой:
![]()
Показатель адиабаты всегда больше 1, поэтому при адиабатическом сжатии газа – как идеального, так и реального – до меньшего объема температура газа всегда возрастает, а при расширении газ охлаждается. Это свойство адиабатического процесса, называемое пневматическим огнивом, применяется в дизельных двигателях, где горючая смесь сжимается в цилиндре и воспламеняется от высокой температуры. Вспомним первый закон термодинамики: ![]() , где
, где ![]() — внутренняя энергия системы, а А – выполняемая над ней работа. Поскольку
— внутренняя энергия системы, а А – выполняемая над ней работа. Поскольку ![]() то работа, осуществляемая газом, идёт только на изменение его внутренней энергии – а значит, температуры. Из уравнения Пуассона можно получить формулу для расчёта работы газа в адиабатном процессе:
то работа, осуществляемая газом, идёт только на изменение его внутренней энергии – а значит, температуры. Из уравнения Пуассона можно получить формулу для расчёта работы газа в адиабатном процессе:
![]()
Здесь n – количество газа в молях, R – универсальная газовая постоянная, Т – абсолютная температура газа.
Уравнение Пуассона для адиабатического процесса применяется не только при расчётах двигателей внутреннего сгорания, но и в проектировании холодильных машин.
Стоит помнить, что уравнение Пуассона точно описывает только равновесный адиабатный процесс, состоящий из непрерывно сменяющих друг друга состояний равновесия. Если же мы в реальности откроем кран в баллоне, чтобы газ адиабатически расширился, возникнет нестационарный переходной процесс с завихрениями газа, которые затухнут из-за макроскопического трения.
Примеры решения задач
| Задание | Одноатомный идеальный газ адиабатически сжали так, что его объем увеличился в 2 раза. Как изменится давление газа? |
| Решение | Показатель адиабаты для одноатомного газа равен где R – универсальная газовая постоянная, а і – степень свободы молекулы газа. Для одноатомного газа степень свободы равен 3: это значит, что центр молекулы может совершать поступательные движения по трём координатным осям. 
Поэтому показатель адиабаты: Представим состояния газа в начале и конце адиабатного процесса через уравнение Пуассона: |
| Ответ | Давление уменьшится в 3,175 раза. |
| Задание | 100 молей двухатомного идеального газа адиабатически сжали при температуре 300 К. При этом давление газа увеличилось в 3 раза. Как изменилась работа газа? |
| Решение | Степень свободы двухатомной молекулы 
Рассчитаем показатель адиабаты двухатомного газа: Определим, как изменился объем газа при адиабатном сжатии, из уравнения Пуассона: Значит, объем газа уменьшился в 2,19 раза. Вычислим работу газа с помощью следующей формулы:
|
| Ответ |











