Деформации. Силы упругости. Закон Гука
Деформация и ее виды
Пластическими деформациями называются деформации, полностью или частично сохраняющиеся после прекращения действии внешних сил.
Способность к упругим и пластическим деформациям зависит от природы вещества, из которого состоит тело, условий, в которых оно находится; способов его изготовления. Например, если взять разные сорта железа или стали, то у них можно обнаружить совершенно разные упругие и пластичные свойства. При обычных комнатных температурах железо является очень мягким, пластичным материалом; закаленная сталь, наоборот, — твердый, упругий материал. Пластичность многих материалов представляет собой условие для их обработки, для изготовления из них нужных деталей. Поэтому она считается одним из важнейших технических свойств твердого вещества.
При деформации твердого тела происходит смещение частиц (атомов, молекул или ионов) из первоначальных положений равновесия в новые положения. При этом изменяются силовые взаимодействия между отдельными частицами тела. В результате в деформированном теле возникают внутренние силы, препятствующие его деформации.
Различают деформации растяжения (сжатия), сдвига, изгиба, кручения.
Силы упругости
Силы упругости имеют электромагнитную природу. Они препятствуют деформациям и направлены перпендикулярно поверхности соприкосновения взаимодействующих тел, а если взаимодействуют такие тела, как пружины, нити, то силы упругости направлены вдоль их оси.
Силу упругости, действующую на тело со стороны опоры, часто называют силой реакции опоры.
Абсолютное удлинение:
![]()
где ![]() и
и ![]() длина тела в деформированном и недеформированном состоянии соответственно.
длина тела в деформированном и недеформированном состоянии соответственно.
Относительное удлинение:
![]()
Закон Гука
Небольшие и кратковременные деформации с достаточной степенью точности могут рассматриваться как упругие. Для таких деформаций справедлив закон Гука:
- Сила упругости, возникающая при деформации тела прямо пропорциональна абсолютному удлинению тела и направлена в сторону, противоположную смещению частиц тела:
![Rendered by QuickLaTeX.com \[F_x=-kx\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7499e62f2008d4957080b74a8e8d7427_l3.png)
где ![]() проекция силы на ось
проекция силы на ось ![]() жесткость тела, зависящая от размеров тела и материала, из которого оно изготовлено, единица жесткости в системе СИ Н/м.
жесткость тела, зависящая от размеров тела и материала, из которого оно изготовлено, единица жесткости в системе СИ Н/м.
Примеры решения задач
| Задание | Пружина жесткостью |
| Решение | Сделаем рисунок.
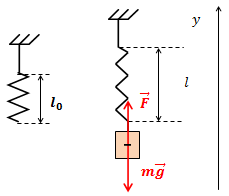
На груз, подвешенный на пружине, действуют сила тяжести Спроектировав это векторное равенство на координатную ось или По закону Гука сила упругости: поэтому можно записать: откуда длина деформированной пружины: Переведем в систему СИ значение длины недеформированной пружины Ускорение свободного падения Подставив в формулу численные значения физических величин, вычислим: |
| Ответ | Длина деформированной пружины составит 29 см. |
| Задание | По горизонтальной поверхности передвигают тело массой 3 кг с помощью пружины жесткостью |
| Решение | Сделаем рисунок.
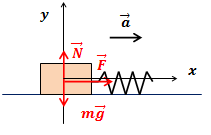
На тело действуют сила тяжести Выберем систему координат, как показано на рисунке и запишем это векторное равенство в проекциях на оси координат: Для решения задачи воспользуемся первым уравнением системы. По закону Гука сила упругости пружины: Ускорение тела: Таким образом: откуда абсолютное удлинение пружины: |
| Ответ | Пружина удлинится на 1,5 см. |






![Rendered by QuickLaTeX.com \[ \begin{cases} F=ma\ \ \ \left(x\right) \\ N-mg=0\ \left(y\right) \end{cases} \right\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-69461a4ccb6ca2e7180b7098938d55fb_l3.png)





