Закон упругой деформации

ОПРЕДЕЛЕНИЕ

Деформация является упругой, в том случае, если она полностью исчезает при прекращении действия деформирующей силы.

Упругая деформация переходит неупругую (пластическую), перейти предел упругости. При упругой деформации частицы, смещенные в новые положения равновесия в кристаллической решетке, после снятия деформирующей силы занимают в старые места. Тело полностью восстанавливает свои размеры и форму после снятия нагрузки.

Закон упругой деформации

Английский естествоиспытатель Р. Гук опытным путем получил, прямую связь между деформирующей силой (F) и удлинением деформированной пружины (x). Внешняя сила порождает силы упругости тела. Эти силы равны по величине, сила упругости уравновешивает действие силы деформации. Закон Гука записывают как:

$x=\frac{1}{k}F_x \qquad (1)$

где $F_x$ – проекция силы на ось X; x- удлинение пружины по оси X; k – коэффициент упругости пружины (жесткость пружины). При использовании такой величины, как сила упругости ( $F_{upr}$ ) для деформированной пружины, то закон Гука приобретает вид:

$F_{upr,\ x}=-kx \qquad (2)$

где $F_{upr,\ x}$ – проекция силы упругости на ось X. Коэффициент k – это величина, зависящая от материала, размеров витка пружины и ее длины. Закон Гука справедлив для малых удлинений и небольших нагрузок.

Закон упругой деформации справедлив для растяжения (сжатия) упругого стержня. Обычно, в этом случае, упругие силы в стержне описывают при помощи напряжения $\sigma$ .

$\sigma =\frac{F_{upr,\ \bot}}{S} \qquad (3)$

При этом считают, что сила распределяется равномерно по сечению и она перпендикулярна поверхности сечения. $\sigma {\rm >0}$ , если происходит растяжение и $\sigma {\rm <0}$ при сжатии. Напряжение $\sigma$ называют нормальным. При этом тангенциальное напряжение $\tau$ равно:

$\tau =\frac{F_{upr,\ ||}}{S} \qquad (4)$

где $F_{upr,\ ||}$ — сила упругости, которая действует вдоль слоя тела; S – площадь рассматриваемого слоя.

Изменение длины стержня ( $\Delta l$ ) равно:

$\Delta l=\frac{1}{k}\sigma =\frac{l\sigma}{E} \qquad (5)$

где E – модуль Юнга; l – длина стержня. Модуль Юнга характеризует упругие свойства материала.

Закон упругой деформации при сдвиге

Сдвигом, называют такую деформацию, при которой плоские слои твердого тела смещаются параллельно друг другу. При таком виде деформации слои не изменяют свою форму и размер. Мерой данной деформации служит угол сдвига ( $\gamma$ ) или величина сдвига ( $\Delta s$ ). Закон Гука для упругой деформации сдвига записывают как:

$\Delta s=\frac{Fh}{GS}$

или

$\tau =G\gamma \qquad (6)$

где G – модуль поперечной упругости (модуль сдвига), h — толщина деформируемого слоя; $\gamma$ – угол сдвига.

Все виды упругой деформации могут сводиться к деформациям растяжения или сжатия, которые происходят одномоментно.

Примеры решения задач

ПРИМЕР 1

Задание

Стальной стержень нагревают от температуры 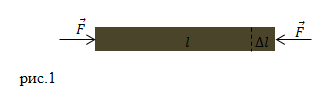$T_1=273$ K до $T_2=303$ K. При этом для того чтобы он не увеличивал свою длину его сжимают с силой F. Чему равна данная сила, приложенная к обоим концам стержня, если площадь его поперечного сечения равна $S={10}^{-3}m^2$ ?

Решение

Исходя из закона упругой деформации (закон Гука) стержень следует сжимать с силой раной:

$F=\frac{\Delta l}{l}ES \qquad (1.1)$

Удлинение стержня, которое возникает при его нагревании, найдем как:

$\Delta l=l\alpha \left(T_2-T_1\right) \qquad (1.2)$

Подставим правую часть выражения (1.2) в закон Гука, имеем:

$F=\frac{l\alpha \left(T_2-T_1\right)}{l}ES=\alpha \left(T_2-T_1\right)ES$

Модуль Юнга для стали примем равным $E=2\cdot {10}^{11}$ Па, коэффициент линейного температурного расширения стали $\alpha =12,5\cdot {10}^6\frac{1}{grad}$ . Проведем вычисления:

$F=12,5\cdot {10}^{-6}\left(303-273\right)\cdot 2\cdot {10}^{11}\cdot {10}^{-3}=75000\ (N)$

Ответ

$F=75000$ Н

ПРИМЕР 2

Задание

Какова длина проволоки из меди, если ее подвесили вертикально, и она начала рваться под воздействием собственной силы тяжести?

Решение

Для того чтобы проволока начала разрушаться должно выполняться условие:

$\frac{mg}{S}\ge {\sigma}_{max} \qquad (2.1)$

где ${\sigma}_{max}=245\cdot {10}^6$ Па – предел прочности меди. Если проволока только начала рваться, то предельный случай запишем как:

${\sigma}_{max}=\frac{mg}{S} \qquad (2.2)$

Массу проволоки выразим как:

$m=\rho V=\rho Sl \qquad (2.3)$

где $\rho$ – плотность меди. Подставим правую часть выражения (2.3) в (2.2), выразим длину проволоки:

${\sigma}_{max}=\frac{\rho Slg}{S}=\rho lg\ \to l=\frac{{\sigma}_{max}}{\rho g}$

Вычислим длину проволоки, зная, что плотность меди равна $\rho =8900\ \frac{kg}{m^3}$ :

$l=\frac{245\cdot {10}^6}{8900\cdot 9,8}=2,8\cdot {10}^3(m)$

Ответ

$l=2,8\cdot {10}^3$ м

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Закон упругой деформации

Закон упругой деформации

Закон упругой деформации при сдвиге

Примеры решения задач