Свойства треугольников
Все свойства треугольников
В любом треугольнике три угла и три стороны.
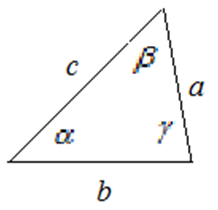
Сумма углов любого треугольника равна ![]() .
.
Против большего угла треугольника лежит большая сторона.
Треугольники бывают остроугольными (если все его углы острые), тупоугольными (если один из его углов тупой), прямоугольными (если один из его углов прямой).
Треугольник называется равносторонним, если все три стороны равны.
Основные линии треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.
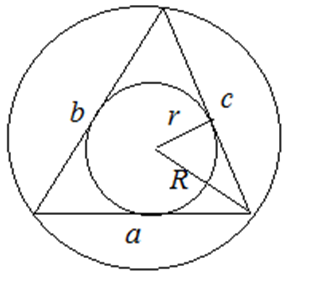
В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.
Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.
Признаки равенства треугольников
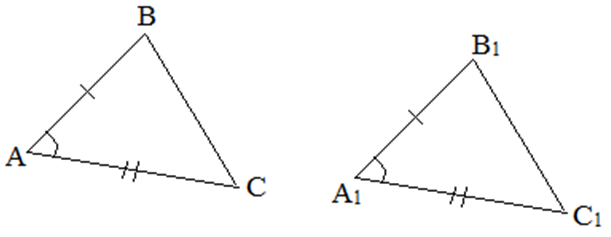
I признак. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
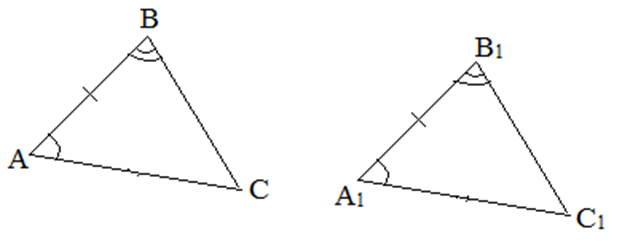
II признак. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
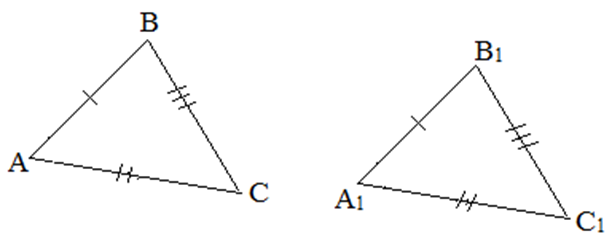
III признак. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Треугольники называются подобными, если их стороны пропорциональны.
Признаки подобия треугольников
- Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
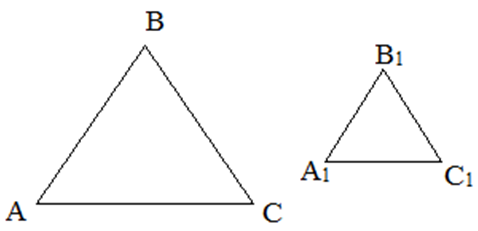
- Если три стороны одного треугольника пропорциональны двум сторонам другого треугольника, то такие треугольники подобны.
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
![]()
Подробнее про теорему косинусов по ссылке.
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности (обобщенная теорема синусов):
![]()
Подробнее про теорему синусов по ссылке.
Площадь треугольника можно вычислить по формулам
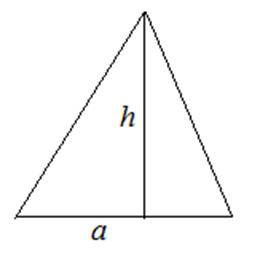
1. Через высоту и основание
![]()
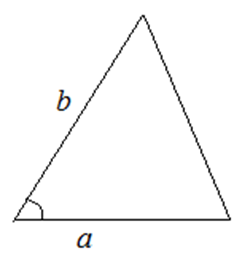
2. По двум сторонам и углу между ними
![]()
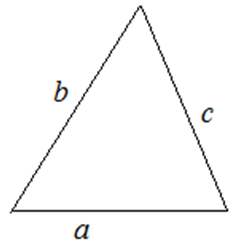
3. По формуле Герона
![]()
где ![]() – полупериметр треугольника
– полупериметр треугольника
4. Через радиусы вписанной и описанной окружностей
![]()
где ![]() – полупериметр треугольника,
– полупериметр треугольника, ![]() – радиус вписанной окружности;
– радиус вписанной окружности;
![]()
![]() – радиус описанной окружности.
– радиус описанной окружности.
Примеры решения задач
| Задание | В треугольнике 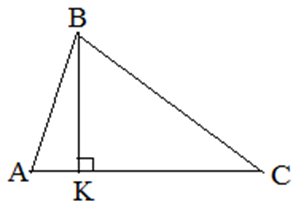
|
| Решение | Высота Рассмотрим прямоугольный треугольник Площадь треугольника |
| Ответ |
| Задание | В треугольнике 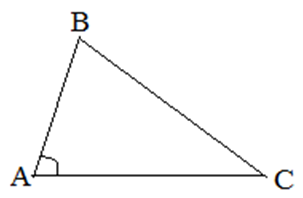
|
| Решение | Найдем сторону откуда Углы треугольника найдем, используя теорему синусов: Откуда Далее найдем |
| Ответ |











