Свойства медианы треугольника
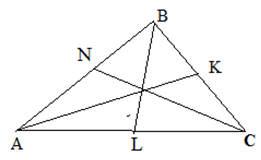
Свойства медиан треугольника
- Медиана разбивает треугольник на два равновеликих треугольника (т.е. на треугольники с одинаковой площадью).
- Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, начиная от вершины. Эта точка называется центром тяжести треугольника.
- Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
- В равнобедренном треугольнике медиана, опущенная на основание, является биссектрисой и высотой.
- В равностороннем треугольнике любая медиана является высотой и биссектрисой.
Примеры решения задач
| Задание | В равнобедренном треугольнике 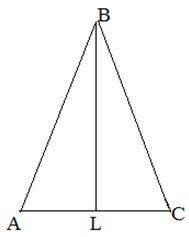
|
| Решение | Медиана делит треугольник на два равновеликих треугольника, тогда Найдем площадь треугольника С помощью теоремы Пифагора найдем катет Подставим полученные результаты в формулу площади: Теперь найдем площадь треугольника |
| Ответ |
| Задание | В треугольнике 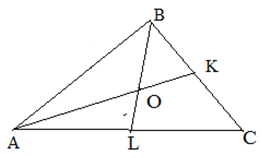
|
| Решение | Так как Рассмотрим треугольник Медианы |
| Ответ |











