Свойства равнобедренного треугольника
ОПРЕДЕЛЕНИЕ
Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья – основанием треугольника.
Свойства равнобедренного треугольника
- В равнобедренном треугольнике углы при основании равны:
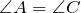
- В равнобедренном треугольнике медиана, проведенная к основанию, является одновременно и биссектрисой, и высотой треугольника:
![\[BK\bot AC, \quad AK=KC, \quad \angle ABK=\angle CBK\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-75381c53deaa8468b5cb3d11fd52353d_l3.png "Rendered by QuickLaTeX.com")
Примеры решения задач
ПРИМЕР 1
| Задание | В равнобедренном треугольнике  боковая сторона в четыре раза больше основания, а его периметр равен 27 см . Найти длину боковой стороны.
|
| Решение | В заданном треугольнике обозначим основание  , тогда боковые стороны  .
Найдем периметр треугольника: откуда |
| Ответ |  см
|
![\[{{P}_{ABC}}=AB+BC+AC=4x+4x+x=9x=27\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-44aad49caac9a658c1e4ca6afe3355ae_l3.png "Rendered by QuickLaTeX.com")
, Таким образом, получаем ![\[AB=BC=4\cdot 3=12 \ cm\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d5502b08a732e6c45899e92c63f4f070_l3.png "Rendered by QuickLaTeX.com")
ПРИМЕР 2
| Задание | В равнобедренном треугольнике с основанием  провели медиану  . Найдите угол  , если  .
|
| Решение | В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой, а это значит что
Рассмотрим прямоугольный треугольник |
| Ответ | 
|
![\[\angle ABK=\angle KBC={{50}^{\circ}}, \quad \angle AKB={{90}^{\circ}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b682ff3656ab8a6d13201c1c371a3a45_l3.png "Rendered by QuickLaTeX.com")
, в котором ![\[\angle A={{180}^{\circ}}-{{90}^{\circ}}-{{50}^{\circ}}={{40}^{\circ}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-a3a628676d84bf51fd2986d238d48fa2_l3.png "Rendered by QuickLaTeX.com")
