Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Свойства Свойства средней линии треугольника

Свойства средней линии треугольника

ОПРЕДЕЛЕНИЕ

Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.

Свойства средней линии треугольника

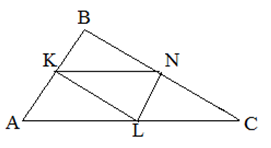
Средняя линия треугольника параллельна одной стороне и равна ее половине. Например, на рисунке
$KN||AC, \quad KN=\frac{1}{2}AC$
В любом треугольнике три средних линии, при пересечении которых образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.
Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четвёртой площади исходного треугольника.

Примеры решения задач

ПРИМЕР 1

Задание

В треугольнике 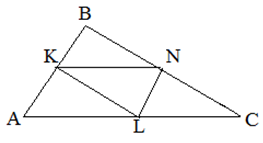$ABC$ со сторонами $AB=5$ см, $B=7$ см и $AC=8$ см провели средние линии $KN, \quad NL$ и $KL$ . Найти периметр треугольника $KNL$ .

Решение

Так как средняя линия равна половине стороны, которой она параллельна, то можем найти длины все средних линий:

$KN=\frac{1}{2}AC=4\ cm, \quad NL=\frac{1}{2}AB=2,5\ cm, \quad KL=\frac{1}{2}=3,5\ cm$

Теперь можно найти периметр треугольника $KNL$ как сумму длин всех его сторон:

${{P}_{KNL}}=KN+NL+KL=4+2,5+3,5=10\ cm$

Ответ

${{P}_{KNL}}=10$ см

ПРИМЕР 2

Задание

В треугольнике 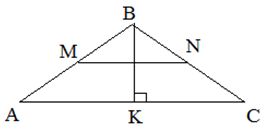$ABC$ со стороной $AC=7$ см и высотой $BK=4$ см провели среднюю линию $MN$ , параллельную стороне $AC$ . Найти площадь треугольника $MBN$ .

Решение

Средняя линия $MN$ отсекает треугольник $MBN$ , площадь которого равна одной четвёртой площади исходного треугольника $ABC$ . Найдем площадь треугольника $ABC$ :

${{S}_{ABC}}=\frac{1}{2}AC\cdot BK=\frac{1}{2}7\cdot 4=14 \ {{cm}^{\text{2}}}$

Тогда площадь треугольника $MBN$ равна:

${{S}_{MBN}}=\frac{1}{4}{{S}_{ABC}}=\frac{1}{4}\cdot 14=3,5 \ {{cm}^{\text{2}}}$

Ответ

${{S}_{MBN}}=3,5$ см $^{2}$

Читайте также:

Свойства окружности вписанной в треугольник

Свойства окружности описанной около треугольника

Свойства высоты

Свойства вписанного угла

Свойства внешнего угла треугольника

© SolverBook - онлайн сервисы для учебы, 2015

Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Почта для связи: info@ru.solverbook.com

Выберите язык:

Сервисы

SolverBook