Свойства биссектрисы треугольника
ОПРЕДЕЛЕНИЕ
Биссектриса угла треугольника – это луч, который исходит из вершины треугольника и делит данный угол пополам.
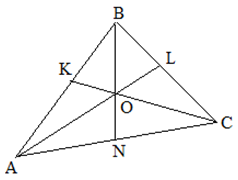
ОПРЕДЕЛЕНИЕ
Три биссектрисы треугольника пересекаются в одной точке, которая называется инцентром треугольника.
ОПРЕДЕЛЕНИЕ
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой, находящейся на противолежащей стороне.
Свойства биссектрисы угла треугольника
- Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам:
![Rendered by QuickLaTeX.com \[\frac{CL}{LB}=\frac{AC}{AB}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7ceda5652ffc18f846cef29228897ca7_l3.png)
- Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в этот треугольник.
- Биссектриса угла – это геометрическое место точек, равноудаленных от сторон этого угла.
- Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.
- В правильном треугольнике биссектриса является медианой и высотой.
Примеры решения задач
ПРИМЕР 1
| Задание | В треугольнике 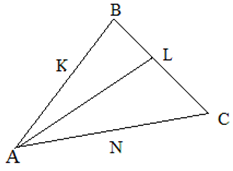
|
| Решение | Биссектриса Если в последнее равенство подставить данные из условия задачи, то получим следующую пропорцию: откуда |
| Ответ |
ПРИМЕР 2
| Задание | В треугольнике |
| Решение | Сумма углов в любом треугольнике равна 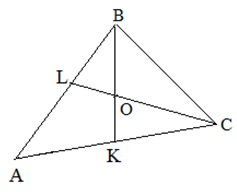
Рассмотрим треугольник Из этого следует, что |
| Ответ |











