Построение гиперболы

Схема построения графика гиперболы

Функцию, которую можно задать формулой вида $y=\frac{k}{x}$ называют обратной пропорциональностью. Кривая, которая является графиком функции $y=\frac{k}{x}$ , называется гиперболой.

Гипербола состоит из двух частей – веток гиперболы. Если $k>0$ , то ветви гиперболы расположены в I и III координатных четвертях, а если $k<0$ – то в II и IV четвертях.

Областью определения и областью значений функции $y=\frac{k}{x}$ , где $k\ne 0$ , есть все числа, кроме 0. Гипербола не имеет общих точек с осью ординат.

Функция $y=\frac{k}{x}$ – нечетная функция, поскольку

$f(-x)=\frac{k}{-x} =-\frac{k}{x} =-f(x),$

значит, график функции симметричен относительно начала координат.

Если $k>0$ , то функция убывает на промежутке $(-\infty ,0)\bigcup (0,+\infty )$ .

Если $k<0$ , то функция возрастает на промежутке $(-\infty ,0)\bigcup (0,+\infty )$ .

Примеры решения задач

ПРИМЕР 1

Задание

Построить график функции $y=\frac{1}{x}$

Решение

Поскольку 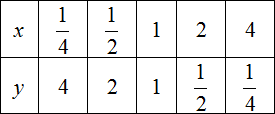$k=1>0$ , то гипербола будет расположена в I и III координатных четвертях. Сначала построим ветвь графика на промежутке $(0,+\infty )$ . Составим таблице значений функции

Нанесем полученные точки на координатную плоскость и соединим их плавной линией. Это будет ветвь графика функции 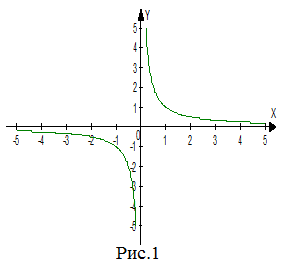$y=\frac{1}{x}$ на промежутке $(0,+\infty )$ . Воспользовавшись нечетностью функции, добавим к построенной ветви ветвь, симметричную относительно начала координат. Получим график функции $y=\frac{1}{x}$ (рис. 1).

ПРИМЕР 2

Задание	Решить уравнение $\frac{4}{x} =x+3$
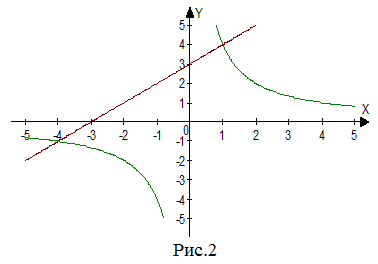
Решение	Сделаем рисунок. Рассмотрим функции $y=\frac{4}{x}$ и $y=x+3$ . Построим в одной системе координат графики этих двух функции (рис. 2) – гиперболу и прямую. Они пресекаются в двух точках, абсциссы которых равны 1 и (-4). В точках пресечения графиков функций сами функции принимают одинаковые значения. Значит, при найденных абсциссах значения выражений $\frac{4}{x}$ и $x+3$ равны, т.е. числа 1 и -4 являются корнями исходного уравнения $\frac{4}{x} =x+3$ .
Ответ	Корни исходного уравнения: $1, -4$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Построение гиперболы

Схема построения графика гиперболы

Примеры решения задач