Кубическая парабола
ОПРЕДЕЛЕНИЕ
Кубическая парабола является графиком функции 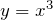 .
.
Свойства кубической параболы
- Область определения и область значений функции – вся числовая прямая.
- Функция
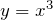 – нечетная:
– нечетная:
![Rendered by QuickLaTeX.com \[f(-x)=(-x)^{3} =-x^{3} =-f(x),\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f352db20e7b2ab5bab96daf28ccd1c88_l3.png)
- Функция
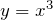 возрастает на всей числовой прямой и является непрерывной.
возрастает на всей числовой прямой и является непрерывной.
а, значит, ее график симметричен относительно начала координат.
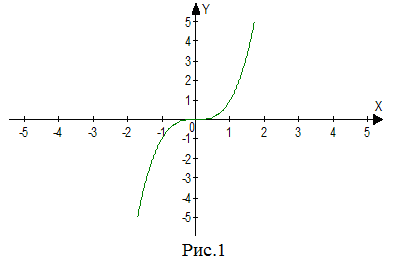
График кубической параболы
График кубической параболы изображен на рисунке 1.
Примеры решения задач
ПРИМЕР 1
| Задание | Построить график функции |
| Решение | Графиком функции 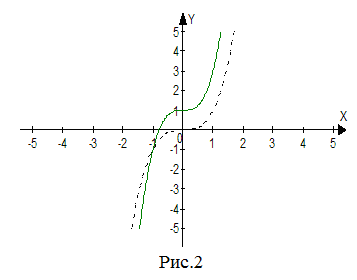
|
ПРИМЕР 2
| Задание | Найти площадь фигуры, ограниченной линиями |
| Решение | Фигура, ограниченная линиями 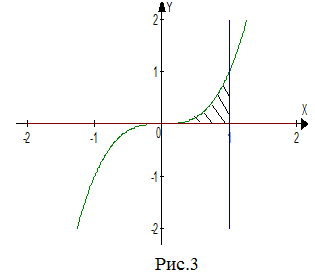
Функция 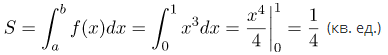
|
| Ответ | 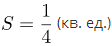 |











