Построение параболы

Алгоритм построения графика параболы

Если парабола задана уравнением $y=ax^{2} +bx+c$ , то чтобы построить ее график, понадобится:

Выяснить направление ветвей параболы: если коэффициент 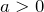$a>0$ , то ветви направлены вверх, а если 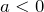$a<0$ – вниз.
Определить координаты вершины параболы. Чтобы определить абсциссу вершины параболы пользуются формулой
$x_{bep} =-\frac{b}{2a}$

Для определения ординаты вершины параболы нужно подставить в уравнение параболы вместо 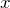$x$ найденное в предыдущем шаге значение $x_{bep}$ :

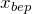$y_{bep} =y\left(x_{bep} \right)=a\cdot x_{bep}^{2} +b\cdot x_{bep} +c$
Нанести полученную точку на график и провести через неё ось симметрии, параллельно координатной оси $Oy$ .
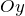Найти точки пересечения с осями координат:

– с осью $Ox$ – найти корни уравнения $ax^{2} +bx+c=0$ , если уравнение не имеет действительных корней, то график не пересекает ось абсцисс,

– с осью $Oy$ – подставить в уравнение значение $x=0$ и вычислить значение $y$ .

Найти координаты произвольной точки 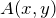$A(x,y)$ , которая принадлежит параболе. Для этого возьмем произвольное значение 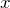$x$ и подставим его в уравнение параболы.
Соединить полученные точки на графике плавной линией и продолжить график за крайние точки, до конца координатной оси.

Примеры решения задач

ПРИМЕР 1

Задание

Построить график функции $y=x^{2}$

Решение

Графиком функции $y=x^{2}$ является парабола, ветви которой направлены вверх (т.к. старший коэффициент $a=1>0$ ), а вершина находится в начале координат. Осью симметрии является ось $Oy$ .

Найдем дополнительные точки. Возьмем значение $x=1$ и подставим в уравнение параболы:

$y=x^{2} =1^{2} =1$

То есть получили точку с координатами 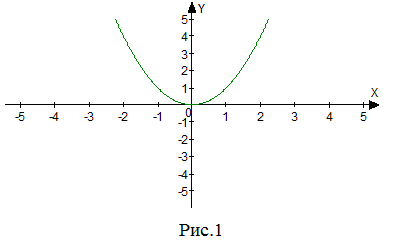$(1,1)$ . Аналогично найдем еще несколько точек параболы: (-1,1), (2,4), (-2,4).

График функции $y=x^{2}$ изображен на рисунке 1.

ПРИМЕР 2

Задание

Построить график функции $y=-2x^{2} +3x+2$

Решение

График функции является парабола. Ветви параболы направлены вниз, так как коэффициент $a=-2<0$ . Найдем координаты вершины параболы:

$x_{bep} =-\frac{b}{2a} =\frac{3}{4} ,\ y_{bep} =-2\cdot \left(\frac{3}{4} \right)^{2} +3\cdot \left(\frac{3}{4} \right)+2=\frac{25}{8}$

Осью симметрии будет прямая $x=\frac{3}{4}$ .

Найдем точки пересечения с осями координат

– с осью 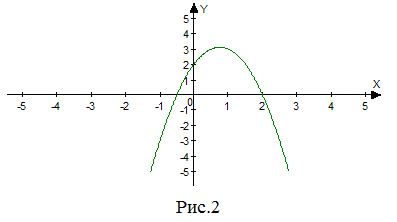$Ox$ . Корнями уравнения $-2x^{2} +3x+2=0$ будут $x_{1} =2,\ x_{2} =-\frac{1}{2}$ . Следовательно, точки пересечения с осью $Ox$ : $(2,0)$ и $\left(-\frac{1}{2} ,0\right)$ ;