График гиперболы

Определение и график гиперболы

ОПРЕДЕЛЕНИЕ

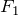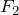Гиперболой называется геометрическое место точек плоскости, для которой абсолютная величина разности расстояний до двух фиксированных точек $F_{1}$ и $F_{2}$ этой плоскости, называемых фокусами, есть величина постоянная.

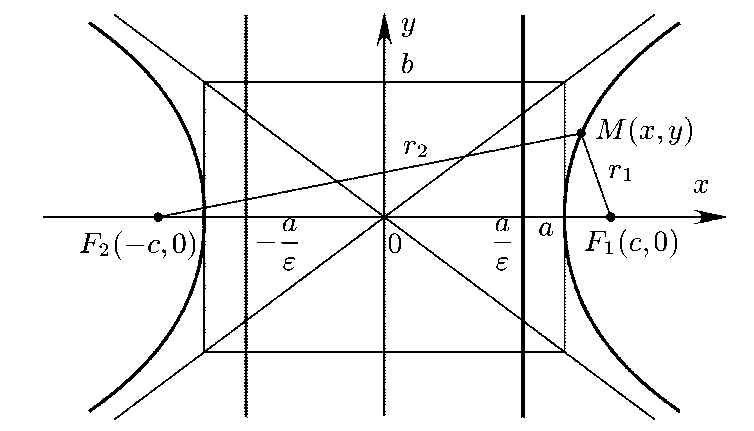
График гиперболы изображен на рисунке 1.

Примеры решения задач

ПРИМЕР 1

Задание

Построить график гиперболы

$\frac{x^{2} }{9} -\frac{y^{2} }{25} =1$

Решение

Из уравнения следует, что действительная ось гиперболы 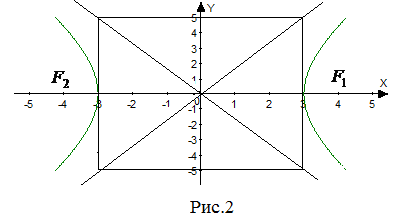$a=3$ , а мнимая ось $b=5$ , а вершины гиперболы имеют координаты $(3,0)$ и $(-3,0)$ . Асимптотами гиперболы будут прямые

$y=\pm \frac{b}{a}, x=\pm \frac{5}{3} x$

График гиперболы $\frac{x^{2} }{9} -\frac{y^{2} }{25} =1$ изображен на рисунке 2.

ПРИМЕР 2

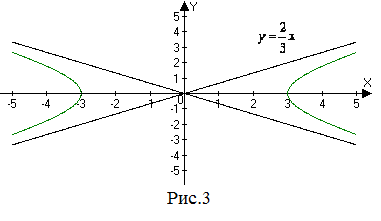
Задание

По графику, изображенному на рисунке 3, записать уравнение кривой.

Решение

На рисунке 3 изображена гипербола, действительная ось которой $a=3$ . Асимптотами гиперболы являются прямые $y=\pm \frac{2}{3} x$ . Из уравнений асимптот найдем значение параметра $b$ :

$y=\pm \frac{b}{a} x=\pm \frac{2}{3} x\Rightarrow b=2$

Тогда уравнение гиперболы имеет вид

$\frac{x^{2} }{9} -\frac{y^{2} }{4} =1$

Ответ

$\frac{x^{2} }{9} -\frac{y^{2} }{4} =1$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

График гиперболы

Определение и график гиперболы

Примеры решения задач