Гипербола
Определение гиперболы
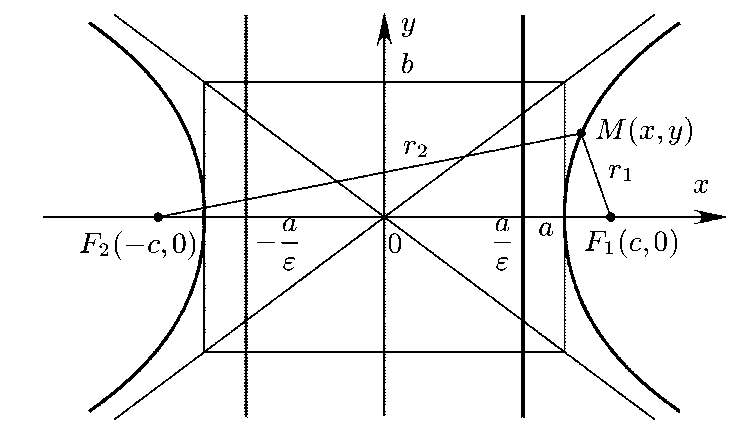
Фокусы ![]() и
и ![]() гиперболы естественно считать различными, т.к. если указанная в определении постоянная не равна нулю, то нет ни одной точки плоскости при совпадении
гиперболы естественно считать различными, т.к. если указанная в определении постоянная не равна нулю, то нет ни одной точки плоскости при совпадении ![]() и
и ![]() , которая бы удовлетворяла требованиям определения гиперболы. Если же эта постоянная равна нулю и
, которая бы удовлетворяла требованиям определения гиперболы. Если же эта постоянная равна нулю и ![]() совпадает с
совпадает с ![]() , то любая точка плоскости удовлетворяет требованиям определения гиперболы.
, то любая точка плоскости удовлетворяет требованиям определения гиперболы.
Каноническое уравнение гиперболы
Гипербола имеет каноническое уравнение
![]()
где ![]() . Действительная полуось гиперболы равна
. Действительная полуось гиперболы равна ![]() , а мнимая полуось равна
, а мнимая полуось равна ![]() .
.
Вершинами гиперболы называются точки ![]() .
.
Фокусы гиперболы имеют координаты ![]() и
и ![]() , где
, где ![]() .
.
Эксцентриситетом гиперболы называется величина ![]() , равная
, равная
![]()
Для гиперболы величина ![]() .
.
Директрисы гиперболы задаются уравнениями
![]()
Асимптотами гиперболы являются прямые ![]() .
.
Гипербола ![]() называется сопряженной к гиперболе
называется сопряженной к гиперболе ![]() , она имеет те же асимптоты, но ее ветви расположены в другой паре вертикальных углов между асимптотами.
, она имеет те же асимптоты, но ее ветви расположены в другой паре вертикальных углов между асимптотами.
Примеры решения задач
| Задание | Найти полуоси, эксцентриситет и координаты фокусов гиперболы
|
| Решение | Полуоси Эксцентриситет гиперболы тогда эксцентриситет будет равен Фокусы гиперболы имеют координаты
|
| Ответ |
| Задание | Составить уравнения директрис и асимптот гиперболы
|
| Решение | Директрисы гиперболы задаются уравнениями Тогда уравнения директрис запишутся в виде: Асимптотами гиперболы являются прямые |
| Ответ |











