Свойства гиперболы
Определение и свойства гиперболы
![]()
Указанная система координат называется канонической, а уравнение – каноническим уравнением гиперболы.
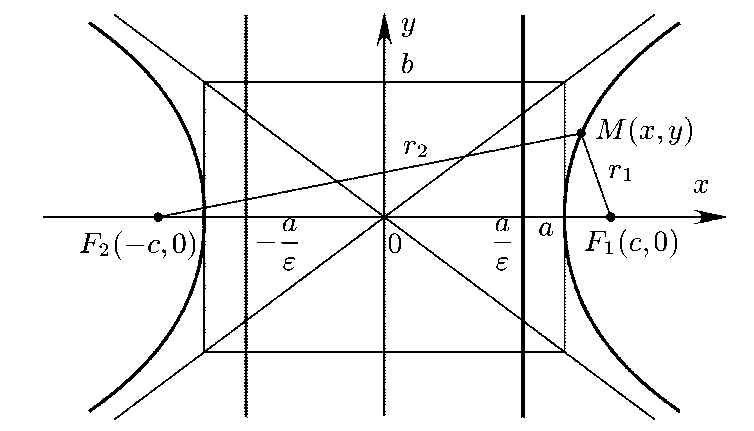
Фокальное свойство гиперболы. Гипербола является геометрическим местом точек, разность расстояний от которых до фокусов по абсолютной величине постоянна:
![]()
Директориальное свойство гиперболы. Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно числу ![]() , называемому эксцентриситетом гиперболы.
, называемому эксцентриситетом гиперболы.
Прямые ![]() называются директрисами гиперболы.
называются директрисами гиперболы.
Примеры решения задач
| Задание | Составить каноническое уравнение гиперболы, если эксцентриситет гиперболы равен |
| Решение | Выберем вершину гиперболы с координатами
Также известно, что эксцентриситет гиперболы равен Получили два условия на
Подставим полученные результаты в каноническое уравнение гиперболы и получим |
| Ответ | 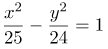 |
| Задание | Составить уравнение директрис гиперболы, если эксцентриситет |
| Решение | Директрисы гиперболы задаются уравнениями откуда Так как точка откуда |
| Ответ | Уравнение директрис гиперболы: |











