Уравнение гиперболы
Каноническое уравнение гиперболы
Каноническое уравнение гиперболы имеет вид
![]()
где ![]() – вещественная полуось,
– вещественная полуось, ![]() – мнимая полуось гиперболы.
– мнимая полуось гиперболы.
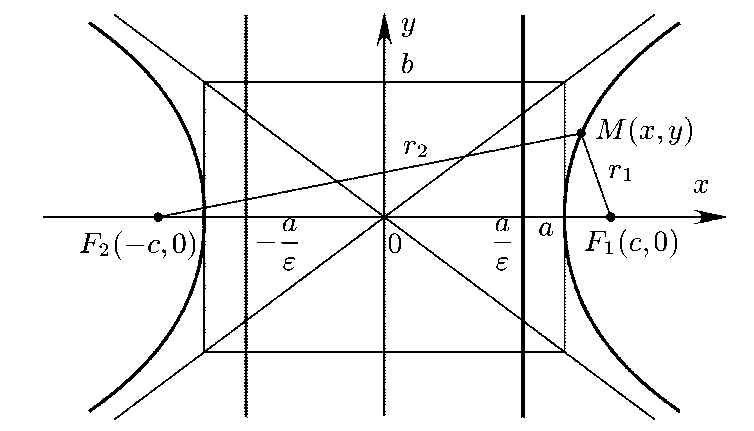
Вершины гиперболы находятся на вещественной оси и имеют координаты ![]() . Фокусы гиперболы имеют координаты
. Фокусы гиперболы имеют координаты ![]() и
и ![]() , где
, где ![]() .
.
Примеры решения задач
| Задание | Составить уравнение гиперболы, если длина вещественной оси равна единице, а точка |
| Решение | Из условия задачи известно, что длина вещественной оси равна единице, тогда параметр Найдем значение параметра Подставим полученное значение в уравнение гиперболы |
| Ответ | Уравнение гиперболы имеет вид: |
| Задание | В данной системе координат гипербола имеет каноническое уравнение. Составить это уравнение, если расстояние между вершинами равно 10, а расстояние между фокусами равно 12. |
| Решение | Вершины гиперболы имеют координаты Фокусы гиперболы имеют координаты Найдем значение параметра Теперь можно записать искомое уравнение гиперболы |
| Ответ | 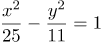 |






![Rendered by QuickLaTeX.com \[\frac{x^{2} }{\left(\frac{1}{2} \right)^{2} } -\frac{y^{2} }{b^{2} } =1 \Rightarrow 4x^{2} -\frac{y^{2} }{b^{2} } =1\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9d597eb08a403b7648231d7a199a3d29_l3.png)





