Извлечение корня из комплексного числа

Невозможно однозначно извлечь корень из комплексного числа, поскольку он имеет число значений, равное его степени.

Комплексные числа возводят в степень в тригонометрической форме, для которой верна формула Муавра:

$z^{k} = r^{k} (\cos k \varphi + i \sin k \varphi),\text{ } \forall k \in N$

Аналогично применяют данную формулу для вычисления корня степени $k$ из комплексного числа (не равного нулю):

$z^{\frac{1}{k}} = \left( r (\cos (\varphi + 2\pi n) + i \sin ( \varphi + 2\pi n) ) \right)^{\frac{1}{k}} =$

$= r^{\frac{1}{k}} \left( \cos \frac{\varphi + 2\pi n}{k} + i \sin \frac{\varphi + 2\pi n}{k} \right), \text{ } \forall k >1 , \text{ } \forall n \in N , \text{ } n < k$

Если комплексное число не равно нулю, то корни степени $k$ существуют всегда, и их можно изобразить на комплексной плоскости: они будут представлять собой вершины $k$ -угольника, который вписан в окружность с центром в начале координат и радиусом $r^{\frac{1}{k}}$ .

Примеры решения задач

ПРИМЕР 1

Задание

Найти корень 3-й степени из числа $z=-1$ .

Решение

Для начала выразим число $z=-1$ в тригонометрической форме. Действительной частью числа $z=-1$ является число $x = \text{Re } z=-1$ , мнимой частью является $y = \text{Im } z=0$ . Для нахождения тригонометрической формы записи комплексного числа нужно найти его модуль и аргумент.

Модулем комплексного числа $z$ является число:

$r=\sqrt{x^{2}+y^{2}}=\sqrt{(-1)^{2}+0^{2}}=\sqrt{1+0}=1$

Аргумент вычисляется по формуле:

$\varphi = \arg z = \text{arctg } \frac{y}{x} = \text{arctg } \frac{0}{-1} = \text{arctg } 0 = \pi$

Следовательно, тригонометрическая форма комплексного числа имеет вид: $z = 1 \left( \cos \pi + i \sin \pi \right)$ .

Тогда корень 3-й степени находится следующим образом:

$z^{\frac{1}{3}} = \left( 1 \left( \cos \pi + i \sin \pi \right) \right)^{\frac{1}{3}} = 1^{\frac{1}{3}} \left( \cos \pi + i \sin \pi \right) ^{\frac{1}{3}} =$

$= \cos \frac{\pi + 2 \pi n}{3} + i \sin \frac{\pi + 2 \pi n}{3}, \text{ }n=0, 1, 2$

Для $n=0$ получаем:

$\omega _{1} = \cos \frac{\pi}{3} + i \sin \frac{\pi}{3} = \frac{1}{2} + i \frac{\sqrt{3}}{2}$

Для $n=1$ получаем:

$\omega _{2} = \cos \pi + i \sin \pi= -1+i \cdot 0 = -1$

Для $n=2$ получаем:

$\omega _{3} = \cos \frac{5\pi}{3} + i \sin \frac{5\pi}{3} = \frac{1}{2} + i \frac{-\sqrt{3}}{2} = \frac{1}{2} - i \frac{\sqrt{3}}{2}$

Ответ

ПРИМЕР 2

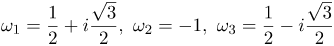Задание

Извлечь корень 2-й степени из числа $z=1-\sqrt{3}i$ .

Решение

Для начала выразим комплексное число в тригонометрической форме.

Действительной частью комплексного числа $z=1-\sqrt{3}i$ является число $x=\text{Re }z=1$ , мнимой частью является $y=\text{Im }z=-\sqrt{3}$ . Для нахождения тригонометрической формы записи комплексного числа нужно найти его модуль и аргумент.

Модулем комплексного числа $r$ является число:

$r=\sqrt{x^{2}+y^{2}}=\sqrt{1^{2}+(-\sqrt{3})^{2}}=\sqrt{1+3}=2$

Аргумент равен:

$\varphi = \arg z = \text{arctg } \frac{y}{x} = \text{arctg } \frac{-\sqrt{3}}{1} = \text{arctg } (-\sqrt{3}) = \frac{2 \pi}{3}$

Следовательно, тригонометрическая форма комплексного числа имеет вид:

$z = 2 \left( \cos \frac{2 \pi}{3} + i \sin \frac{2 \pi}{3} \right)$

Применяя формулу для извлечения корня 2-й степени, получаем:

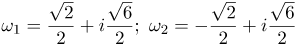$z^{\frac{1}{2}} = \left( 2 \left( \cos \frac{2 \pi}{3} + i \sin \frac{2 \pi}{3} \right) \right)^{\frac{1}{2}} = 2^{\frac{1}{2}} \left( \cos \frac{2 \pi}{3} + i \sin \frac{2 \pi}{3} \right) ^{\frac{1}{2}} =$

$= \sqrt{2} \left( \cos \left( \frac{\pi}{3} + \pi n \right) + i \sin \left( \frac{\pi}{3} + \pi n \right) \right), \text{ }n=0, 1$

Для $n=0$ получаем:

$\omega _{1} = \sqrt{2} \left( \cos \left( \frac{\pi}{3} + 0 \right) + i \sin \left( \frac{\pi}{3} + 0 \right) \right) = \sqrt{2} \left( \frac{1}{2} + i \frac{\sqrt{3}}{2} \right) = \frac{\sqrt{2}}{2} + i \frac{\sqrt{6}}{2}$

Для $n=1$ получаем:

$\omega _{2} = \sqrt{2} \left( \cos \left( \frac{\pi}{3} + \pi \right) + i \sin \left( \frac{\pi}{3} + \pi \right) \right) = \sqrt{2} \left( -\frac{1}{2} + i \frac{\sqrt{3}}{2} \right) = -\frac{\sqrt{2}}{2} + i \frac{\sqrt{6}}{2}$

Ответ

Понравился сайт? Расскажи друзьям!