Модуль комплексного числа

Если рассмотреть плоскость с прямоугольной системой координат, то любому комплексному числу $z=x+iy$ можно сопоставить точку на этой плоскости с соответствующими координатами: $\left\{ x, y \right\}$ , и радиус-вектор $r$ комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу.

Данная плоскость называется комплексной. Действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси.

ОПРЕДЕЛЕНИЕ

Модулем комплексного числа $z=x+iy$ называется выражение $r=|z|=\sqrt{x^{2}+y^{2}}$ .

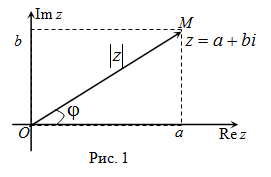
Таким образом, модуль вычисляется как квадратный корень из суммы квадратов действительной и мнимой частей комплексного числа.

ПРИМЕР

Задание	Найти модуль числа $z=-5+15i$ .
Решение	Действительной частью комплексного числа $z=-5+15i$ является число $x = \text{Re } z = -5$ , мнимой частью является $y = \text{Im } z=15$ . Следовательно, модуль числа – это выражение: $r=\sqrt{x^{2}+y^{2}} = \sqrt{(-5)^{2}+15^{2}}=\sqrt{25+225}=\sqrt{250}$
Ответ	$r=\sqrt{250}$

Если $z$ является действительным числом, то его модуль $r=|z|$ равен абсолютной величине этого действительного числа.

Например. $z=-17, \text{ }r=|-17|=17$

Свойства модуля

Модуль комплексного числа не отрицателен: 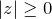$|z| \geq 0$ , при этом 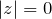$|z|=0$ в том и только том случае, если $z=0$ ;
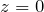Модуль суммы двух комплексных чисел меньше либо равен сумме модулей: $|z_{1}+z_{2}| \leq |z_{1}|+|z_{2}|$ ;
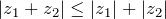Модуль произведения двух комплексных чисел равен произведению модулей: 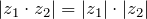$|z_{1} \cdot z_{2}| = |z_{1}| \cdot |z_{2}|$ , в том числе $|q \cdot z_{2}| = q \cdot |z_{2}|, \text{ }q \in R$ ;
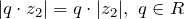Модуль частного двух комплексных чисел равен частному модулей: $|z_{1} \div z_{2}| = |z_{1}| \div |z_{2}|$ ;
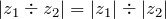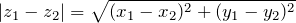$|z_{1}-z_{2}| = \sqrt{(x_{1}-x_{2})^{2} + (y_{1}-y_{2})^{2}}$ , т.е. модуль разности комплексных чисел равен расстоянию между этими числами на комплексной плоскости.

Примеры решения задач

ПРИМЕР 1

Задание

Найти частное модулей комплексных чисел $z_{1}=15i, \text{ }z_{2}=1+i$ .

Решение

Модуль комплексного числа $z_{1}=15i$ равен $r_{1}=\sqrt{0^{2}+15^{2}}=15$ , модуль комплексного числа $z_{2}=1+i$ равен $r_{2}=\sqrt{1^{2}+1^{2}}=\sqrt{2}$ .

Следовательно, частное модулей равно:

$r_{1} \div r_{2} = \frac{15}{\sqrt{2}} = 7,5 \sqrt{2} \approx 10,6066$

Ответ

$r_{1} \div r_{2}= 7,5 \sqrt{2} \approx 10,6066$

ПРИМЕР 2

Задание

Найти расстояние между числами $z_{1}=1-3i,\text{ }z_{2}=-2+2i$ на комплексной плоскости.

Решение

Расстояние между двумя комплексными числами находится как модуль разности комплексных чисел. Применяя соответствующую формулу, получаем:

$|z_{1}-z_{2}| = \sqrt{(x_{1}-x_{2})^{2} + (y_{1}-y_{2})^{2}} = \sqrt{(1-(-2))^{2} + (-2-2)^{2}} = \sqrt{34}$

Ответ

Расстояние между комплексными числами $z_{1}=1-3i,\text{ }z_{2}=-2+2i$ равно $\sqrt{34}$ .

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Модуль комплексного числа

Свойства модуля

Примеры решения задач