Геометрическая интерпретация комплексного числа
Комплексные числа можно изображать на комплексной плоскости следующим образом: действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси.
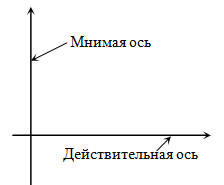
Любому комплексному числу ![]() можно сопоставить точку на этой плоскости с соответствующими координатами:
можно сопоставить точку на этой плоскости с соответствующими координатами: ![]() , и радиус-вектор
, и радиус-вектор ![]() (существуют также обозначения
(существуют также обозначения ![]() ) комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу.
) комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу.
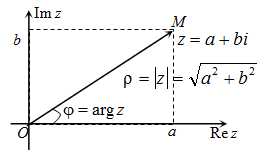
Модуль комплексного числа
Т.е. нужно извлечь квадратный корень из суммы квадрат вещественной и мнимой частей.
| Задание | Найти модуль числа |
| Решение | Действительной частью комплексного числа Следовательно, модуль числа – это выражение |
| Ответ |
Если ![]() является действительным числом, то его модуль
является действительным числом, то его модуль ![]() равен абсолютной величине этого действительного числа.
равен абсолютной величине этого действительного числа.
Например. ![]()
Свойства модуля
- Модуль комплексного числа не отрицателен:
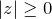 , при этом
, при этом 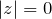 в том и только том случае, если
в том и только том случае, если 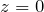 ;
; - Модуль суммы двух комплексных чисел меньше либо равен сумме модулей:
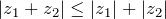 ;
; - Модуль произведения двух комплексных чисел равен произведению модулей:
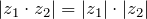 , в том числе
, в том числе 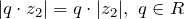 ;
; - Модуль частного двух комплексных чисел равен частному модулей:
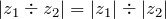 ;
; 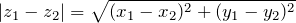 , т.е. модуль разности комплексных чисел равен расстоянию между этими числами на комплексной плоскости.
, т.е. модуль разности комплексных чисел равен расстоянию между этими числами на комплексной плоскости.
| Задание | Найти произведение модулей комплексных чисел |
| Решение | Модуль комплексного числа |
| Ответ |
Аргумент комплексного числа
Свойства аргумента
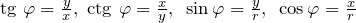
- Для комплексного числа
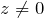 аргумент определяется с точностью до
аргумент определяется с точностью до 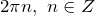 .
.
Для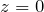 значение аргумента не определено.
значение аргумента не определено. - Главным значением аргумента называется число
![Rendered by QuickLaTeX.com \varphi \in (-\pi; \text{ } \pi]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1cc2555b7871f18493113fccd941b13e_l3.png) . Для обратного числа выполняется свойство:
. Для обратного числа выполняется свойство: 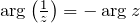 .
.
Два комплексно сопряженных числа имеют равные модули, а их аргументы отличаются знаком.
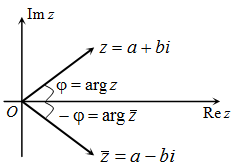
| Задание | Найти аргумент комплексного числа |
| Решение | Действительной частью комплексного числа Аргумент комплексного числа вычисляется по формуле: |
| Ответ | 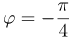 |











