Алгебраическая форма записи комплексного числа

ОПРЕДЕЛЕНИЕ

Алгебраической формой комплексного числа называется запись комплексного числа $z$ в виде $z=x+iy$ , где $x$ и $y$ – действительные числа, $i$ – мнимая единица, удовлетворяющая соотношению $i^{2}=-1$ .

Число $x$ называется действительной частью комплексного числа $z$ и имеет обозначение $x = \text{Re } z$ .

Число $y$ называется мнимой частью комплексного числа $z$ и имеет обозначение $y = \text{Im } z$ .

Например:

Комплексное число 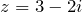$z=3-2i$ и его сопряженное число 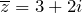$\overline{z}=3+2i$ записаны в алгебраической форме.
Мнимое число 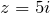$z=5i$ записано в алгебраической форме.

Также, в зависимости от решаемой задачи, вы можете перевести комплексное число в тригонометрическую или показательную форму.

ПРИМЕР

Задание

Записать число $z = \frac{7-i}{4}+13$ в алгебраической форме, найти его действительную и мнимую части, а также сопряженное число.

Решение

Применяя почленное деление дроби и правило сложения дробей, получаем:

$z = \frac{7-i}{4}+13 = \frac{7}{4}+13-\frac{i}{4}=\frac{59}{4}-\frac{1}{4}i$

Следовательно, действительной частью комплексного числа $z = \frac{59}{4}-\frac{1}{4}i$ является число $x = \text{Re } z=\frac{59}{4}$ , мнимой частью является число $y = \text{Im } z=-\frac{1}{4}$ .

Сопряженное число имеет вид: $\overline{z} =\frac{59}{4}+\frac{1}{4}i$ .

Ответ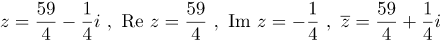

Действия над комплексными числами в алгебраической форме

Сравнение

Два комплексных числа $z_{1}=x_{1}+iy_{1}$ и $z_{2}=x_{2}+iy_{2}$ называются равными, если $x_{1}=x_{2},\text{ } y_{1}=y_{2}$ , т.е. равны их действительные и мнимые части.

ПРИМЕР

Задание	Определить, при каких $x$ и $y$ два комплексных числа $z_{1}=13+yi$ и $z_{2}=x+5i$ являются равными.
Решение	По определению два комплексных числа являются равными, если равны их действительные и мнимые части, т.е. $x=13, \text{ }y=5$ .
Ответ	$x=13, \text{ }y=5$

Сложение

Сложение комплексных чисел $z_{1}=x_{1}+iy_{1}$ и $z_{2}=x_{2}+iy_{2}$ выполняется непосредственным суммированием действительных и мнимых частей:

$z_{1}+z_{2} = x_{1}+iy_{1} + x_{2}+iy_{2} = (x_{1}+x_{2}) + i (y_{1}+y_{2})$

ПРИМЕР

Задание

Найти сумму комплексных чисел $z_{1}=-7+5i, \text{ }z_{2}=13-4i$ .

Решение

Действительной частью комплексного числа $z_{1}=-7+5i$ является число $x_{1} = \text{Re } z_{1}=-7$ , мнимой частью является число $y_{1} = \text{Im } z_{1}=5$ . Действительная и мнимая части комплексного числа $z_{2}=13-4i$ равны $x_{2} = \text{Re } z_{2}=13$ и $y_{2} = \text{Im } z_{2}=-4$ , соответственно.

Следовательно, сумма комплексных чисел равна:

$z_{1}+z_{2} = (x_{1}+x_{2}) + i (y_{1}+y_{2}) = (-7+13)+i(5-4)=6+i$

Ответ

$z_{1}+z_{2} = 6+i$

Подробнее про сложение комплексных числе читайте в отдельной статье: Сложение комплексных чисел.

Вычитание

Вычитание комплексных чисел $z_{1}=x_{1}+iy_{1}$ и $z_{2}=x_{2}+iy_{2}$ выполняется непосредственным вычитанием действительных и мнимых частей:

$z_{1}-z_{2} = x_{1}+iy_{1} - (x_{2}+iy_{2}) = x_{1}-x_{2} + (i y_{1}-iy_{2}) = (x_{1}-x_{2}) + i (y_{1}-y_{2})$

ПРИМЕР

Задание

Найти разность комплексных чисел $z_{1}=17-35i, \text{ }z_{2}=15+5i$ .

Решение

Найдем действительные и мнимые части комплексных чисел $z_{1}=17-35i, \text{ }z_{2}=15+5i$ :

$x_{1} = \text{Re } z_{1}=17 \text{ },\text{ } x_{2} = \text{Re } z_{2}=15$

$y_{1} = \text{Im } z_{1}=-35 \text{ },\text{ } y_{2} = \text{Im } z_{2}=5$

Следовательно, разность комплексных чисел равна:

$z_{1}-z_{2} = (x_{1}-x_{2}) + i (y_{1}-y_{2}) = (17-15)+i(-35-5)=2-40i$

Ответ

$z_{1}-z_{2} = 2-40i$

Умножение

Умножение комплексных чисел $z_{1}=x_{1}+iy_{1}$ и $z_{2}=x_{2}+iy_{2}$ выполняется непосредственным произведением чисел в алгебраической форме, учитывая свойство мнимой единицы $i^{2}=-1$ :

$z_{1} \cdot z_{2} = (x_{1}+iy_{1}) \cdot (x_{2}+iy_{2}) = x_{1} \cdot x_{2} + i^{2} \cdot y_{1} \cdot y_{2} + (x_{1} \cdot iy_{2} + x_{2} \cdot iy_{1}) =$

$= (x_{1} \cdot x_{2} - y_{1} \cdot y_{2}) + i (x_{1} \cdot y_{2} + x_{2} \cdot y_{1})$

ПРИМЕР

Задание	Найти произведение комплексных чисел $z_{1}=1-5i, \text{ }z_{2}=5+2i$ .
Решение	Произведение комплексных чисел равно: $z_{1} \cdot z_{2} = (x_{1} \cdot x_{2} - y_{1} \cdot y_{2}) + i (x_{1} \cdot y_{2} + x_{2} \cdot y_{1}) = (1 \cdot 5 - (-5) \cdot 2 ) + i (1 \cdot 2 + (-5) \cdot 5) = 15-23i$
Ответ	$z_{1} \cdot z_{2} = 15-23i$

Подробнее про умножение комплексных чисел читайте в отдельной статье: Умножение комплексных чисел.

Деление

Частное комплексных чисел $z_{1}=x_{1}+iy_{1}$ и $z_{2}=x_{2}+iy_{2}$ находится путем домножения числителя и знаменателя на сопряженное число к знаменателю:

$\frac{z_{1}}{z_{2}} = \frac{x_{1}+iy_{1}}{x_{2}+iy_{2}} = \frac{(x_{1}+iy_{1})(x_{2}-iy_{2})}{(x_{2}+iy_{2})(x_{2}-iy_{2})}=\frac{x_{1} \cdot x_{2} + y_{1} \cdot y_{2}}{x_{2}^{2}+y_{2}^{2}} + i \frac{x_{2} \cdot y_{1} - x_{1} \cdot y_{2}}{x_{2}^{2}+y_{2}^{2}}$

ПРИМЕР

Задание	Разделить число 1 на комплексное число $z=1+2i$ .
Решение	Поскольку мнимая часть вещественного числа 1 равна нулю, частное чисел равно: $\frac{1}{1+2i} = \frac{1 \cdot 1}{1^{2}+2^{2}} - i \frac{1 \cdot 2}{1^{2}+2^{2}} = \frac{1}{5}-i \frac{2}{5}$
Ответ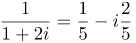

Подробнее про деление комплексных чисел читайте в отдельной статье: Деление комплексных чисел.

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Алгебраическая форма записи комплексного числа

Действия над комплексными числами в алгебраической форме

Сравнение

Сложение

Вычитание

Умножение

Деление