Деление комплексных чисел
Существует три формы записи комплексных чисел: алгебраическая, тригонометрическая и показательная. Рассмотрим деление комплексных чисел в каждой из форм.
Деление в алгебраической форме
Частное комплексных чисел ![]() и
и ![]() находится путем домножения числителя и знаменателя на сопряженное число к знаменателю:
находится путем домножения числителя и знаменателя на сопряженное число к знаменателю:
![]()
| Задание | Разделить число |
| Решение | Используя формулу для нахождения частного, получаем:
|
| Ответ |
Деление в тригонометрической форме
Частное комплексных чисел в тригонометрической форме выполняется по формуле:
![]()
Таким образом, чтобы поделить два комплексных числа, нужно поделить их модули и найти разность аргументов.
| Задание | Найти частное комплексных чисел |
| Решение | Частное комплексных чисел равно:
|
| Ответ | 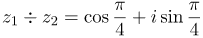 |
Деление в показательной форме
Частное комплексных чисел в показательной форме выполняется по формуле:
![]()
Т.е. чтобы поделить два комплексных числа в показательной форме, нужно найти частное их модулей, а в показателе степени экспоненты найти разность их аргументов.
| Задание | Найти частное комплексных чисел |
| Решение | Частное комплексных чисел равно:
|
| Ответ | 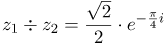 |











