Формы записи комплексных чисел

Существует три формы записи комплексных чисел: алгебраическая, тригонометрическая и показательная. Каждая форма записи удобна для решения своих задач, соответственно вы можете переводить комплексное число из одной формы в другую, в зависимости от решаемой задачи.

Алгебраическая форма комплексного числа

ОПРЕДЕЛЕНИЕ

Алгебраической формой комплексного числа называется запись комплексного числа $z$ в виде $z=x+iy$ , где $x$ и $y$ – действительные числа, $i$ – мнимая единица.

Например:

Комплексное число 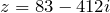$z=83-412i$ и его сопряженное число 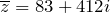$\overline{z}=83+412i$ записаны в алгебраической форме.
Мнимое число 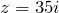$z=35i$ записано в алгебраической форме.

Подробнее про алгебраическую форму читайте в отдельной статье: Алгебраическая форма комплексного числа.

Тригонометрическая форма комплексного числа

ОПРЕДЕЛЕНИЕ

Тригонометрической формой комплексного числа $z=x+iy$ , не равного нулю, называется запись $z = r (\cos \varphi + i \sin \varphi)$ где $r=\sqrt{x^{2}+y^{2}}$ — модуль комплексного числа $z$ .

Ниже мы подробно распишем, как вычислять модуль и аргумент комплексного числа и приведем примеры.

ПРИМЕР

Задание

Выразить число $z=-1+i$ в тригонометрической форме.

Решение

Действительной частью комплексного числа $z=-1+i$ является число $x = \text{Re } z=-1$ , мнимой частью является $y = \text{Im } z=1$ . Для нахождения тригонометрической формы записи комплексного числа нужно найти его модуль и аргумент.

$r=\sqrt{x^{2}+y^{2}}=\sqrt{(-1)^{2}+1^{2}}=\sqrt{2}$

Аргумент вычисляется по формуле:

$\varphi = \arg z = \text{arctg } \frac{y}{x} = \text{arctg } \frac{1}{-1} = \text{arctg } (-1) = -\frac{\pi}{4}$

Следовательно, тригонометрическая форма комплексного числа имеет вид:

$z = \sqrt{2} \left( \cos \left( -\frac{\pi}{4} \right) + i \sin \left( -\frac{\pi}{4} \right) \right)$

Ответ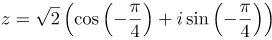

Подробнее про тригонометрическую форму читайте в отдельной статье: Тригонометрическая форма комплексного числа.

Модуль и аргумент комплексного числа

ОПРЕДЕЛЕНИЕ

Модулем комплексного числа $z=x+iy$ называется выражение $r=|z|=\sqrt{x^{2}+y^{2}}$ .

ПРИМЕР

Задание	Найти модуль числа $z=-73+5i$ .
Решение	Действительной частью комплексного числа $z=-73+5i$ является число $x = \text{Re } z=-73$ , мнимой частью является $y = \text{Im } z=5$ . Следовательно, модуль числа – это выражение $r=\sqrt{x^{2}+y^{2}}=\sqrt{(-73)^{2}+5^{2}}=73,17103$
Ответ	$r=73,17103$

Если $z$ является действительным числом, то его модуль $r=|z|$ равен абсолютной величине этого действительного числа.

Например. $z=-57, \text{ }r=|-57|=57$

ОПРЕДЕЛЕНИЕ

Угол $\varphi$ (измеряемый в радианах) радиус-вектора точки, которая соответствует комплексному числу $z$ на комплексной плоскости, называется аргументом числа $z: \varphi = \arg z$ . В таком случае вещественные числа $x, y$ комплексного числа $z=x+iy$ можно выразить через модуль $r$ и аргумент $\varphi: x = r \cos \varphi, y = r \sin \varphi$ .

Показательная форма комплексного числа

ОПРЕДЕЛЕНИЕ

Показательной формой комплексного числа называется выражение $z=r e^{i \varphi}$ , где $r=|z|=\sqrt{x^{2}+y^{2}}$ — модуль комплексного числа, $e^{i \varphi}$ — расширение экспоненты на случай, когда показатель степени является комплексным числом.

ПРИМЕР

Задание

Записать комплексное число $z=-2i$ в показательной форме.

Решение

Действительной частью комплексного числа $z=-2i$ является число $x = \text{Re } z=0$ , мнимой частью является $y = \text{Im } z=-2$ . Находим модуль и аргумент комплексного числа:

$r=\sqrt{x^{2}+y^{2}}=\sqrt{0^{2}+2^{2}}=2$

$\varphi = \arg z = \text{arctg } \frac{y}{x} = \text{arctg } \frac{-2}{0} = \text{arctg } (-\infty) = -\frac{\pi}{2}$

Следовательно, показательная форма имеет вид:

$z=r e^{i \varphi} = 2 e^{-\frac{\pi}{2} i}$

Ответ

$z= 2 e^{-\frac{\pi}{2} i}$

Подробнее про показательную форму читайте в отдельной статье: Показательная форма комплексного числа.

Понравился сайт? Расскажи друзьям!