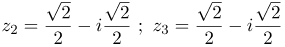Примеры решения комплексных чисел

Теория про комплексные числа

ОПРЕДЕЛЕНИЕ

Комплексным числом называется число вида $z=x+iy$ , где $x$ и $y$ действительные числа, а $i$ – мнимая единица такая, что $i^{2}=-1$ .

При этом такая запись комплексного числа называется алгебраической; $x = \text{Re }(z)$ является действительной частью комплексного числа, а $y = \text{Im }(z)$ – мнимою. Каждое комплексное число может быть так же представлено в тригонометрической форме

$z = r( \cos \varphi + i \sin \varphi)$

или показательной форме:

$z = r e^{i \varphi}$

где $r=|z|=\sqrt{x^{2}+y^{2}}$ – модуль комплексного числа, а $\varphi = \arg z$ – аргумент комплексного числа такой, что $\text{tg }\varphi = \frac{y}{x}$ , где $- \pi \leq \varphi \leq \pi$ или $0 \leq \varphi \leq 2\pi$ .

Комплексные числа изображаются на комплексной плоскости. Для них введены операции сложения, умножения, вычитания и деления. Так же их можно возводить в степень и извлекать из них корень, для этого используют формулу Муавра.

Примеры

ПРИМЕР 1

Задание

Представить в показательной и тригонометрической формах комплексное число $z = 2-2i$ .

Решение

Найдем модуль заданного комплексного числа, по условию действительная часть $x=2$ , а мнимая $y=-2$ , тогда подставляя в формулу для нахождения модуля, получим

$r =\sqrt{x^{2}+y^{2}} = \sqrt{2^{2}+(-2)^{2}} = \sqrt{8} = 2 \sqrt{2}$

Вычислим аргумент заданного комплексного числа:

$\text{tg } \varphi = \frac{-2}{2} \text{ } \Rightarrow \text{ } \text{tg } \varphi = -1 \text{ } \Rightarrow \text{ } \varphi = \text{arctg } (-1) \text{ } \Rightarrow \text{ } \varphi = - \frac{\pi}{4}$

Тогда тригонометрическая форма этого комплексного числа будет иметь вид:

$z = 2 \sqrt{2} \left( \cos \left( - \frac{\pi}{4} \right) + i \sin \left( - \frac{\pi}{4} \right) \right)$

показательная:

$z = 2 \sqrt{2} \cdot e^{- \frac{\pi}{4} i}$

Ответ

ПРИМЕР 2

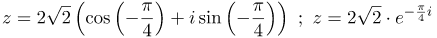Задание

Найти разность и сумму комплексных чисел $z_{1}=1+i$ и $z_{2}=2-3i$ .

Решение

Найдем сумму комплексных чисел, при этом отдельно складываем действительные и мнимые части заданных чисел:

$z_{1}+z_{1} = (1+i)+(2-3i) = (1+2)+(i-3i)=3-2i$

Вычислим разность заданных комплексных чисел, при этом действительные и мнимые части чисел вычитаются отдельно:

$z_{1}-z_{1} = (1+i)-(2-3i) = (1-2)+(i+3i)=-1+4i$

Ответ

$z_{1}+z_{1} =3-2i \text{ };\text{ } z_{1}-z_{1} =-1+4i$

ПРИМЕР 3

Задание

Найти произведение и частное чисел $z_{1}=4+5i$ и $z_{2}=1-i$ .

Решение

Найдем произведение заданных комплексных чисел:

$z_{1} \cdot z_{1} = (4+5i) \cdot (1-i) = 4 \cdot 1 + 5i \cdot 1 + 4 \cdot (-i) + 5i \cdot (-i)=4+5i-4i-5i^{2}$

Учитывая, что $i^{2}=-1$ , окончательно получим:

$z_{1} \cdot z_{1} =4+5i-4i-5i^{2} = 4+i-5 \cdot (-1)=4+i+5=9+i$

Вычислим частное комплексных чисел $z_{1}$ и $z_{2}$ :

$\frac{z_{1}}{z_{2}} = \frac{4+5i}{1-i}$

умножим числитель и знаменатель полученной дроби на сопряженное комплексное число к знаменателю, то есть на $\overline{z_{2}}=1+i$ , получим:

$\frac{z_{1}}{z_{2}} = \frac{(4+5i)(1+i)}{(1-i)(1+i)} = \frac{4+5i+4i+5i^{2}}{1^{2}-i^{2}}$

Учитывая, что $i^{2}=-1$ , окончательно получим:

$\frac{z_{1}}{z_{2}} = \frac{4+5i+4i+5i^{2}}{1^{2}-i^{2}} = \frac{4+9i-5}{1-(-1)}=\frac{-1+9i}{2}=-\frac{1}{2}+\frac{9}{2}i$

Ответ

ПРИМЕР 4

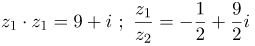Задание

Возвести комплексное число $z=\sqrt{3}+i$ в степень $n$ : а) $n=2$ ; б) $n=6$ .

Решение

а) Возведем заданное комплексное число в квадрат, используя формулы сокращенного умножения:

$z^{2} = (\sqrt{3}+i)^{2} = (\sqrt{3})^{2} + 2\sqrt{3}i+i^{2}=3+2\sqrt{3}i-1=2+2\sqrt{3}i$

б) Для возведения комплексного числа $z=\sqrt{3}+i$ в шестую степень, воспользуемся формулой Муавра. Чтобы её применить, необходимо представить комплексное число в тригонометрической или показательной формах. Найдем модуль заданного комплексного числа:

$r=\sqrt{x^{2}+y^{2}}=\sqrt{(\sqrt{3})^{2} + 1^{2}}=\sqrt{4}=2$

Далее находим его аргумент:

$\text{tg } \varphi = \frac{1}{\sqrt{3}} \text{ } \Rightarrow \text{ } \varphi = \text{arctg } \left( \frac{1}{\sqrt{3}} \right) \text{ } \Rightarrow \text{ } \varphi = \frac{\pi}{6}$

Запишем тригонометрическую форму заданного комплексного числа:

$z=2 \left( \cos \frac{\pi}{6} + i \sin \frac{\pi}{6} \right)$

По формуле Муавра

$z^{6}=2^{6} \left( \cos \frac{6 \cdot \pi}{6} + i \sin \frac{6 \cdot \pi}{6} \right) = 64 \left( \cos \pi + i \sin \pi \right)$

Преобразовывая это выражение, получим алгебраическую форму шестой степени заданного комплексного числа $z=\sqrt{3}+i$ :

$z^{6}= 64 \left( \cos \pi + i \sin \pi \right) = 64 (-1+i \cdot 0) = -64$

Ответ

$z^{2} = 2+2\sqrt{3}i \text{ };\text{ } z^{6}= -64$

ПРИМЕР 5

Задание

Вычислить $\sqrt[4]{-1}$ и изобразить корни на комплексной плоскости.

Решение

Представим число $-1$ в тригонометрической форме, для этого найдем его модуль и аргумент:

$r=|-1|=1$

$\text{tg } \varphi = \frac{0}{-1} \text{ } \Rightarrow \text{ } \varphi = \text{arctg } 0+\pi \text{ } \Rightarrow \text{ } \varphi = 0$

Тогда

$z=1 \cdot \left( \cos \pi + i \sin \pi \right)$

Корни четвертой степени найдем, используя формулу Муавра

$\sqrt[n]{z} = \sqrt[n]{r} \left( \cos \frac{\varphi + 2 \pi k}{n} + i \sin \frac{\varphi + 2 \pi k}{n}\right) \text{ }, \text{ } k = \overline{0, n-1}$

В нашем случае $k=0,1,2,3$ . Найдем значения этого выражения для каждого $k$ :

$z_{0} = \sqrt[4]{1} \left( \cos \frac{\pi + 2 \pi \cdot 0}{4} + i \sin \frac{\pi + 2 \pi \cdot 0}{4}\right) = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} = \frac{\sqrt{2}}{2} + i \frac{\sqrt{2}}{2}$

$z_{1} = \sqrt[4]{1} \left( \cos \frac{\pi + 2 \pi \cdot 1}{4} + i \sin \frac{\pi + 2 \pi \cdot 1}{4}\right) = \cos \frac{3\pi}{4} + i \sin \frac{3\pi}{4} = -\frac{\sqrt{2}}{2} + i \frac{\sqrt{2}}{2}$

$z_{2} = \sqrt[4]{1} \left( \cos \frac{\pi + 2 \pi \cdot 2}{4} + i \sin \frac{\pi + 2 \pi \cdot 2}{4}\right) = \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4} = -\frac{\sqrt{2}}{2} - i \frac{\sqrt{2}}{2}$

$z_{3} = \sqrt[4]{1} \left( \cos \frac{\pi + 2 \pi \cdot 3}{4} + i \sin \frac{\pi + 2 \pi \cdot 3}{4}\right) = \cos \frac{7\pi}{4} + i \sin \frac{7\pi}{4} = \frac{\sqrt{2}}{2} - i \frac{\sqrt{2}}{2}$

Полученные корни можно изобразить на комплексной плоскости. Они будут точками, лежащими на окружности с центром в начале координат и радиусом 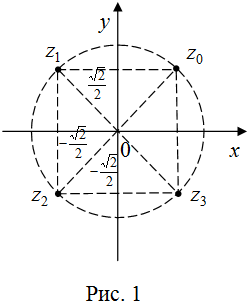$\sqrt[4]{r}=1$ , а центральные углы между радиусами, проведенными в соседние точки, равны $\frac{\pi}{2}$ (рис. 1).

Ответ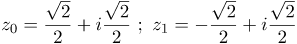

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Примеры решения комплексных чисел

Теория про комплексные числа

Примеры