Комплексно сопряженные числа
| Задание | Найти для комплексного числа |
| Решение | Комплексно сопряженным числом является число вида Следовательно, сопряженное число имеет вид: |
| Ответ |
На комплексной плоскости сопряженные числа зеркально отображены относительно оси вещественных чисел.
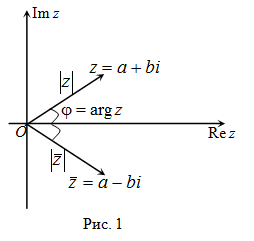
Свойства комплексно сопряженных чисел
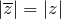 , то есть модули сопряженных чисел равны.
, то есть модули сопряженных чисел равны.
Например. Модуль комплексного числа
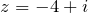 равен
равен 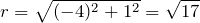 . Сопряженным к комплексному числу будет число
. Сопряженным к комплексному числу будет число 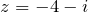 , модуль которого
, модуль которого 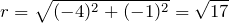 равен модулю исходного числа.
равен модулю исходного числа.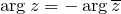 , то есть аргументы сопряженных чисел различаются знаком.
, то есть аргументы сопряженных чисел различаются знаком.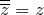 , то есть комплексно сопряженное к сопряженному числу есть исходное комплексное число.
, то есть комплексно сопряженное к сопряженному числу есть исходное комплексное число.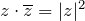 , то есть в результате произведения сопряженных чисел получается вещественное число.
, то есть в результате произведения сопряженных чисел получается вещественное число.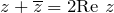 , то есть сумма сопряженных чисел – это тоже вещественное число.
, то есть сумма сопряженных чисел – это тоже вещественное число.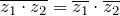 , то есть сопряженное произведения двух комплексных чисел есть произведение их сопряженных чисел.
, то есть сопряженное произведения двух комплексных чисел есть произведение их сопряженных чисел.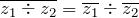 , то есть сопряженное частного чисел есть частное сопряженных.
, то есть сопряженное частного чисел есть частное сопряженных.
Примеры решения задач
| Задание | Умножить комплексное число |
| Решение | Сопряженным к числу |
| Ответ |
| Задание | Найти сопряженное число к частному двух комплексных чисел: |
| Решение | Частное комплексных чисел находится путем домножения числителя и знаменателя на сопряженное число:
Сопряженным числом к частному будет являться число Этот же результат мы получим, если найдем частное сопряженных чисел |
| Ответ | 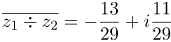 |











