Интеграл от дроби
Нужно запомнить, что интеграл от дроби не равен интегралу числителя, деленному на интеграл знаменателя:
![Rendered by QuickLaTeX.com \[ \int{\frac{f\left( x \right)}{g\left( x \right)}dx}\ne \frac{\int{f\left( x \right)dx}}{\int{g\left( x \right)dx}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-60788e9aa223830e26ed4f14f1d23c22_l3.png)
Для интегрирования подобных выражений существует несколько методов, которые зависят от вида подынтегральной функции.
Первый метод вычисления интеграла от дроби
Подынтегральная функция является отношением двух многочленов и представляет собою неправильную дробь (степень числителя больше или равна степени знаменателя). Тогда нужно выделить целую часть, для этого в числителе либо нужно выделить выражение, стоящее в знаменателе, либо поделить числитель на знаменатель в столбик.
| Задание | Найти интеграл
|
| Решение | Подынтегральная функция представляет собой неправильную дробь, поэтому выделим целую часть. Для этого применим два способа.
1) Поделим числитель на знаменатель в столбик: 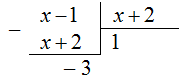
То есть 2) Выделим в числителе выражение, стоящее в знаменателе: Таким образом: Интеграл от разности двух функций равен разности интегралов от каждой из них: |
| Ответ | 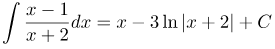 |
Замечание. Если степень многочлена, стоящего в числителе, большее степени многочлена, стоящего в знаменателе, то рациональнее для выделения целой части делить числитель на знаменатель в столбик.
Второй метод
Для дробей типа
![]()
применяется метод замены переменной или заданный интеграл сводится к табличным.
| Задание | Решить интеграл
|
| Решение | Вынесем четверку в знаменателе из-под знака корня:
Свели данный интеграл к табличному, который называется «длинный логарифм»: Тогда для заданного интеграла имеем: |
| Ответ | 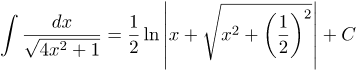 |
Третий метод вычисления интеграла от дроби
Интегралы вида
![]()
находятся с помощью выделения полного квадрата в знаменателе, что позволит свести их к табличным интегралам.
| Задание | Найти интеграл
|
| Решение | Выделим в знаменателе подынтегральной функции полный квадрат:
Сделаем замену переменных: Интеграл принимает вид: Таким образом, свели интеграл к табличному интегралу – «высокий логарифм»: Тогда имеем: Возвращаемся к старой переменной и упрощаем: |
| Ответ | 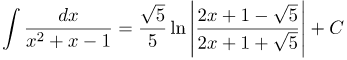 |
Четвертый метод
Для интегралов вида
![]()
применяется следующий подход. В числителе выделяется производная знаменателя, далее дробь почленно делится: получаем сумму двух интегралов, в числителе одного из них стоит производная знаменателя, а второго – константа. Первый из интегралов находится методом замены, метод нахождения второго описан выше.
| Задание | Найти неопределенный интеграл
|
| Решение | Выделим в числителе подынтегральной функции выражение, равное, производной знаменателя Тогда заданный интеграл принимает вид: Для первого интеграла делаем замену переменных: Второй интеграл был найден в предыдущем примере. Итак, имеем: |
| Ответ | 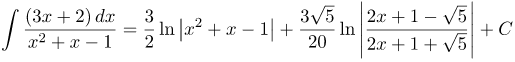 |






![Rendered by QuickLaTeX.com \[\int{\frac{dx}{\sqrt{4{{x}^{2}}+1}}}=\int{\frac{dx}{2\sqrt{{{x}^{2}}+\frac{1}{4}}}}=\frac{1}{2}\int{\frac{dx}{\sqrt{{{x}^{2}}+{{\left( \frac{1}{2} \right)}^{2}}}}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ebaed335a5f1138eb6413d734e223701_l3.png)
![Rendered by QuickLaTeX.com \[\int{\frac{dx}{\sqrt{4{{x}^{2}}+1}}}=\frac{1}{2}\int{\frac{dx}{\sqrt{{{x}^{2}}+{{\left( \frac{1}{2} \right)}^{2}}}}}=\frac{1}{2}\ln \left| x+\sqrt{{{x}^{2}}+{{\left( \frac{1}{2} \right)}^{2}}} \right|+C\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e127090ef42b674777c23fd742d47d2e_l3.png)
![Rendered by QuickLaTeX.com \[\int{\frac{dx}{{{x}^{2}}+x-1}}=\int{\frac{dx}{{{x}^{2}}+2\cdot x\cdot \frac{1}{2}+{{\left( \frac{1}{2} \right)}^{2}}-{{\left( \frac{1}{2} \right)}^{2}}-1}}=\int{\frac{dx}{{{\left( x+\frac{1}{2} \right)}^{2}}-\frac{5}{4}}}=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fbfc99de21705257459e5c77247dbbe5_l3.png)
![Rendered by QuickLaTeX.com \[=\int{\frac{dx}{{{\left( x+\frac{1}{2} \right)}^{2}}-{{\left( \frac{\sqrt{5}}{2} \right)}^{2}}}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-67c36616084b14952c71026d1774d852_l3.png)
![Rendered by QuickLaTeX.com \[\int{\frac{dx}{{{x}^{2}}+x-1}}=\int{\frac{dt}{{{t}^{2}}-{{\left( \frac{\sqrt{5}}{2} \right)}^{2}}}}\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f866417d3e3678df81ae46e58947adb2_l3.png)
![Rendered by QuickLaTeX.com \[\int{\frac{dx}{{{x}^{2}}+x-1}}=\frac{1}{2\cdot \frac{\sqrt{5}}{2}}\ln \left| \frac{t-\frac{\sqrt{5}}{2}}{t+\frac{\sqrt{5}}{2}} \right|+C\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-595547852d0a4f69ff462bdd35ba9534_l3.png)
![Rendered by QuickLaTeX.com \[\int{\frac{dx}{{{x}^{2}}+x-1}}=\frac{\sqrt{5}}{5}\ln \left| \frac{2\left( x+\frac{1}{2} \right)-\sqrt{5}}{2\left( x+\frac{1}{2} \right)+\sqrt{5}} \right|+C=\frac{\sqrt{5}}{5}\ln \left| \frac{2x+1-\sqrt{5}}{2x+1+\sqrt{5}} \right|+C\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-76c9b117d60a71febd4fc502db962dee_l3.png)
![Rendered by QuickLaTeX.com \[\int{\frac{\left( 3x+2 \right)dx}{{{x}^{2}}+x-1}}=\frac{3}{2}\int{\frac{dt}{t}}+\frac{3}{4}\cdot \frac{\sqrt{5}}{5}\ln \left| \frac{2x+1-\sqrt{5}}{2x+1+\sqrt{5}} \right|=\frac{3}{2}\ln \left| t \right|+\frac{3\sqrt{5}}{20}\ln \left| \frac{2x+1-\sqrt{5}}{2x+1+\sqrt{5}} \right|+C=\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-338d7e4697bd244e6e8719fe37973509_l3.png)
![Rendered by QuickLaTeX.com \[=\frac{3}{2}\ln \left| {{x}^{2}}+x-1 \right|+\frac{3\sqrt{5}}{20}\ln \left| \frac{2x+1-\sqrt{5}}{2x+1+\sqrt{5}} \right|+C\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-10eca4c1c5a2b4bd4ac14c9489f66605_l3.png)





