Интеграл разности
Интеграл разности равен разности интегралов
![Rendered by QuickLaTeX.com \[ \int{(f(x) - g(x))dx} = \int{f(x)dx} - \int{g(x)dx} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ec21e1ad8667b1364c2fb7dd9a8341e2_l3.png)
Отметим, что данная формула распространена и на большее конечное число функций, то есть
![]()
Примеры решения задач по теме «Интеграл разности»
| Задание | Найти интеграл |
| Решение | Интеграл разности равен разности интегралов, тогда
а от синуса равен минус косинусу: Тогда искомый интеграл |
| Ответ | 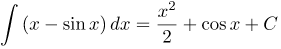 |
| Задание | Решить интеграл |
| Решение | Интеграл разности равен разности интегралов:
Константу можно выносить за знак производной, а интеграл от тангенса Тогда Интеграл степенной функции отсюда имеем: |
| Ответ |











