Интеграл от синуса

Интеграл от синуса равен косинусу того же аргумента плюс константа интегрирования

$\int{\sin xdx}=-\cos x+C$

Примеры решения задач

ПРИМЕР 1

Задание

Найти интеграл $\int{\sin 2x}dx$

Решение

Так как аргумент синуса отличен от переменной интегрирования, то сделаем замену переменных:

$2x=t \text{ } \Rightarrow \text{ } 2dx=dt \text{ } \Rightarrow \text{ } dx=\frac{dt}{2}$

$\int{\sin 2x}dx=\int{\sin t\cdot \frac{dt}{2}}=\frac{1}{2}\int{\sin tdt}=\frac{1}{2}\cdot \left( -\cos t \right)+C=-\frac{1}{2}\cos 2x+C$

Ответ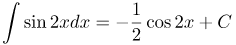

ПРИМЕР 2

Задание	Решить интеграл $\int{\sin (x-1)dx}$
Решение	Применим метод замены переменной: $\int{\sin (x-1)dx}\ \left\\| \begin{matrix} x-1=t \\ dx=dt \\ \end{matrix} \right\\|=\int{\sin t dt}=-\cos t+C=-\cos \left( x-1 \right)+C$
Ответ	$\int{\sin (x-1)dx}=-\cos \left( x-1 \right)+C$

Понравился сайт? Расскажи друзьям!