Интеграл суммы
Интеграл суммы равен сумме интегралов
![Rendered by QuickLaTeX.com \[ \int{(f(x) + g(x))dx} = \int{f(x)dx} + \int{g(x)dx} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-86f3eae7b5b6f1d2542eab8ce3b3c1c3_l3.png)
Данная формула распространена и на большее конечное число слагаемых:
![]()
Примеры решения задач по теме «Интеграл суммы»
| Задание | Найти интеграл
|
| Решение | Интеграл суммы равен сумме интегралов:
Первый интеграл Для второго интеграла используем правило: знак интеграла уничтожает знак дифференциала: Тогда |
| Ответ | 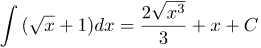 |
| Задание | Решить интеграл |
| Решение | Записываем данный интеграл в виде суммы двух интегралов:
Интеграл косинуса равен синусу: то есть Таким образом, |
| Ответ | 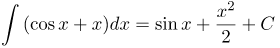 |






![Rendered by QuickLaTeX.com \[\int{\sqrt{x}dx}=\int{x^\frac{1}{2}dx}=\frac{{{x}^{\frac{1}{2}+1}}}{\frac{1}{2}+1}=\frac{{{x}^{\frac{3}{2}}}}{\frac{3}{2}}+C=\frac{2\sqrt{{{x}^{3}}}}{3}+C\]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5eeecc11b252dcae80e74387d6dd177f_l3.png)





